机器学习术语表
本术语表中列出了一般的机器学习术语和 TensorFlow 专用术语的定义。
C
超参数|Hyperparameter
在机器学习中,超参数是在开始学习过程之前设置值的参数,而不是通过训练得到的参数数据。通常情况下,需要对超参数进行优化,给模型选择一组最优超参数,以提高学习的性能和效果。
超平面|Hyperplane
将一个空间划分为两个子空间的边界。例如,在二维空间中,直线就是一个超平面,在三维空间中,平面则是一个超平面。在机器学习中更典型的是:超平面是分隔高维度空间的边界。核支持向量机利用超平面将正类别和负类别区分开来(通常是在极高维度空间中)。
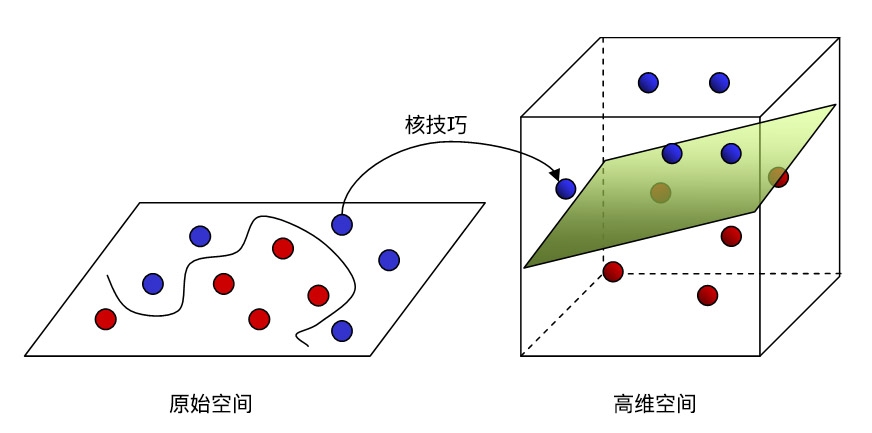
参数|Parameter
机器学习系统自行训练的模型的变量。
例如,权重就是一种参数,它们的值是机器学习系统通过连续的训练迭代逐渐学习到的。参数的概念与超参数相对应。
测试集|Test Set
数据集的子集,用于在模型经过验证集验证之后测试模型。当然,有时候我们不设置验证集(主要用于模型调参),直接使用训练数据训练模型后就进行测试。
D
独热编码|One-Hot Encoding
一种稀疏向量,其中:
- 一个元素设为 1。
- 所有其他元素均设为 0。
One-Hot 编码常用于表示拥有有限个可能值的字符串或标识符。例如,假设某个指定的植物学数据集记录了 15000 个不同的物种,其中每个物种都用独一无二的字符串标识符来表示。在特征工程过程中,您可能需要将这些字符串标识符编码为 One-Hot 向量,向量的大小为 15000。
独立同分布
独立就是每次抽样之间是没有关系的,不会相互影响。
同分布,意味着随机变量 $X_1$ 和 $X_2$ 具有相同的分布形状和相同的分布参数,对离散随机变量具有相同的分布律,对连续随机变量具有相同的概率密度函数,有着相同的分布函数,相同的期望、方差。
例如,某个网页的访问者在短时间内的分布可能为独立同分布,即分布在该短时间内没有变化,且一位用户的访问行为通常与另一位用户的访问行为无关。
迭代|Iteration
模型的权重在训练期间的一次更新,迭代包含计算参数在单个批量数据的梯度损失。
F
泛化|Generalization
指的是模型依据训练时采用的数据,针对以前未见过的新数据做出正确预测的能力。
反向传播算法|Backpropagation
在神经网络上执行梯度下降法的主要算法。该算法会先按前向传播方式计算(并缓存)每个节点的输出值,然后再按反向传播遍历图的方式计算损失函数值相对于每个参数的偏导数。
G
过拟合|Overfitting
创建的模型与训练数据过于匹配,以致于模型无法根据新数据做出正确的预测。
如图,绿线代表过拟合模型,黑线代表正则化模型。虽然绿线完美的匹配训练数据,但太过依赖,并且与黑线相比,对于新的测试数据上具有更高的错误率。
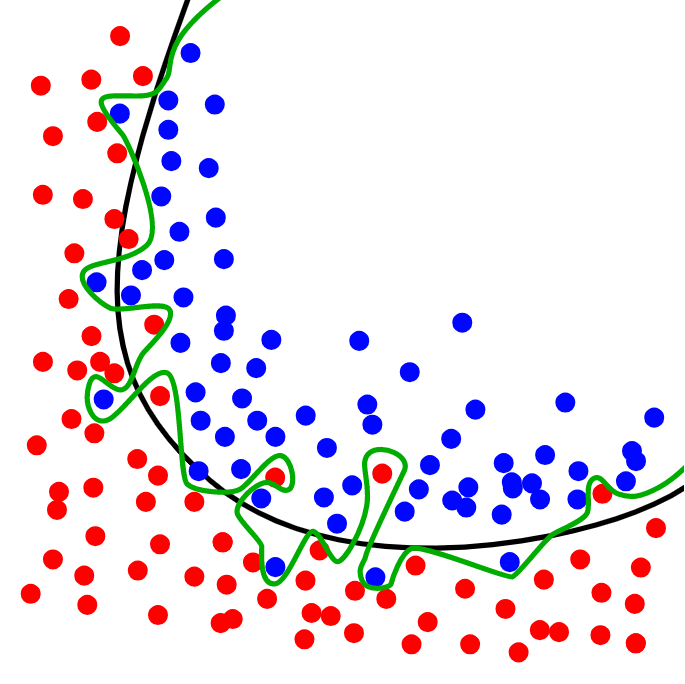
H
混淆矩阵|Confusion Matrix
一种 NxN 表格,用于总结分类模型的预测成效;即标签和模型预测的分类之间的关联。在混淆矩阵中,一个轴表示模型预测的标签,另一个轴表示实际标签。N 表示类别个数。在二元分类问题中,N=2。例如,下面显示了一个二元分类问题的混淆矩阵示例:
| 肿瘤(预测的标签) | 非肿瘤(预测的标签) | |
|---|---|---|
| 肿瘤(实际标签) | 18 | 1 |
| 非肿瘤(实际标签) | 6 | 452 |
上面的混淆矩阵显示,在 19 个实际有肿瘤的样本中,该模型正确地将 18 个归类为有肿瘤(18 个真正例),错误地将 1 个归类为没有肿瘤(1 个假负例)。同样,在 458 个实际没有肿瘤的样本中,模型归类正确的有 452 个(452 个真负例),归类错误的有 6 个(6 个假正例)。
多类别分类问题的混淆矩阵有助于确定出错模式。例如,某个混淆矩阵可以揭示,某个经过训练以识别手写数字的模型往往会将 4 错误地预测为 9,将 7 错误地预测为 1。混淆矩阵包含计算各种效果指标(包括精确率和召回率)所需的充足信息。
J
集成学习|Ensemble
多个模型的预测结果的并集。
通俗来讲,集成学习把大大小小的多种算法融合在一起,共同协作来解决一个问题。集成学习可以用于分类问题集成,回归问题集成,特征选取集成,异常点检测集成等。
你可以通过以下一项或多项来创建集成学习:
- 不同的初始化
- 不同的超参数
- 不同的整体结构
决策边界|Decision Boundary
在二元分类或多类别分类问题中,模型学到的类别之间的分界线。例如,在以下表示某个二元分类问题的图片中,决策边界是橙色类别和蓝色类别之间的分界线:

精确率|Precision
一种分类模型指标。精确率指模型正确预测正类别的频率。
$$
召回率 = \frac { 真正例数 } { 真正例数 + 假负例数 }
$$
交叉熵|Cross-Entropy
对数损失函数向多类别分类问题进行的一种泛化。交叉熵可以量化两种概率分布之间的差异。
$$
H(p,q) = \sum_{i=1}^{n} p(x) \cdot log(\frac{1}{q(x)})
$$
激活函数|Activation Function
一种函数(例如 ReLU 或 S 型函数),用于对上一层的所有输入求加权和,然后生成一个输出值(通常为非线性值),并将其传递给下一层。
结构风险最小化|Structural Risk Minimization
一种算法,用于平衡以下两个目标:
- 期望构建最具预测性的模型(例如损失最低)。
- 期望使模型尽可能简单(例如强大的正则化)。
例如,旨在将基于训练集的损失和正则化降至最低的模型函数就是一种结构风险最小化算法。
L
离群点|Outlier
与大多数其他值差别很大的值。在机器学习中,下列所有值都是离群值。
- 绝对值很高的权重。
- 与实际值相差很大的预测值。
- 值比平均值高大约 3 个标准偏差的输入数据。
离群值常常会导致模型训练出现问题。
类别|Class
为标签枚举的一组目标值中的一个。例如,在检测垃圾邮件的二元分类模型中,两种类别分别是「垃圾邮件」和「非垃圾邮件」。在识别狗品种的多类别分类模型中,类别可以是「贵宾犬」、「小猎犬」、「哈巴犬」等。
离散特征|Discrete Feature
一种特征,包含有限个可能值。例如,某个值只能是「动物」、「蔬菜」或「矿物」的特征便是一个离散特征(或分类特征)。与连续特征相对。
M
密集层|Dense Layer
是全连接层的同义词。
P
批次|Batch
模型训练的一次迭代(即一次梯度更新)中使用样本簇。
偏差|Bias
距离原点的截距或偏移。偏差(也称为偏差项)在机器学习模型中以 $b$ 或 $w_0$ 表示。例如,在下面的公式中,偏差为 $b$:
$$y’ = b + w_1x_1 + w_2x_2 + … w_nx_n$$
请勿与「预测偏差」混淆。
批次规模|Batch Size
模型迭代一次,使用的样本集的大小。
例如训练集有 6400 个样本,batch_size=128,那么训练完整个样本集需要 50 次迭代。Batch Size 的大小一般设置为 16 及 16 的倍数。
R
ROC 曲线下面积
一种会考虑所有可能分类阀值的评价指标。
ROC 曲线下面积的数值意义为:对于随机选择的正类别样本确实为正类别,以及随机选择的负类样本为正类别,分类器更确信前者的概率。
S
输入层|Input Layer
神经网络中的第一层(接受输入数据的层)
输出层|Output Layer
神经网络最后一层。
损失|Loss
一种衡量指标,用于衡量模型的预测偏离其标签的程度。或者更悲观地说是衡量模型有多差。要确定此值,模型必须定义损失函数。例如,线性回归模型通常将均方误差用于损失函数,而逻辑回归模型则使用对数损失函数。
收敛|Convergence
通俗来说,收敛通常是指在训练期间达到的一种状态,即经过一定次数的迭代之后,训练损失和验证损失在每次迭代中的变化都非常小或根本没有变化。也就是说,如果采用当前数据进行额外的训练将无法改进模型,模型即达到收敛状态。在深度学习中,损失值有时会在最终下降之前的多次迭代中保持不变或几乎保持不变,暂时形成收敛的假象。
缩放|Scaling
特征工程中的一种常用做法,是对某个特征的值区间进行调整,使之与数据集中其他特征的值区间一致。例如,假设您希望数据集中所有浮点特征的值都位于 0 到 1 区间内,如果某个特征的值位于 0 到 500 区间内,您就可以通过将每个值除以 500 来缩放该特征。
随机梯度下降法|SGD
SGD 依赖于从数据集中随机均匀选择的单个样本来计算每步的梯度估算值。
Softmax 函数
一种函数,可提供多类别分类模型中每个可能类别的概率。这些概率的总和正好为 1.0。例如,softmax 可能会得出某个图像是狗、猫和马的概率分别是 0.9、0.08 和 0.02。(也称为完整 softmax。)
T
推断|Inference
在机器学习中,推断通常指以下过程:通过将训练过的模型应用于无标签样本来做出预测。在统计学中,推断是指在某些观测数据条件下拟合分布参数的过程。
梯度|Gradient
偏导数相对于所有自变量的向量。在机器学习中,梯度是模型函数偏导数的向量。
梯度下降法|Gradient Descent
一种通过计算并且减小梯度将损失降至最低的技术,它以训练数据为条件,来计算损失相对于模型参数的梯度。通俗来说,梯度下降法以迭代方式调整参数,逐渐找到权重和偏差的最佳组合,从而将损失降至最低。
特征|Feature
在进行预测时使用的输入变量。
特征组合|Feature Cross
通过将单独的特征进行组合(相乘或求笛卡尔积)而形成的合成特征。特征组合有助于表示非线性关系。
特征工程|Feature Engineering
指以下过程:确定哪些特征可能在训练模型方面非常有用,然后将日志文件及其他来源的原始数据转换为所需的特征。
凸函数|Convex Function
一种函数,函数图像以上的区域为凸集。典型凸函数的形状类似于字母 U。例如,以下都是凸函数:

严格凸函数只有一个局部最低点,该点也是全局最低点。经典的 U 形函数都是严格凸函数。不过,有些凸函数(例如直线)则不是这样。
很多常见的损失函数(包括下列函数)都是凸函数:
- L2 损失函数
- 对数损失函数
- L1 正则化
- L2 正则化
梯度下降法的很多变体都一定能找到一个接近严格凸函数最小值的点。同样,随机梯度下降法的很多变体都有很高的可能性能够找到接近严格凸函数最小值的点(但并非一定能找到)。
两个凸函数的和(例如 L2 损失函数 + L1 正则化)也是凸函数。
深度模型绝不会是凸函数。值得注意的是,专门针对凸优化设计的算法往往总能在深度网络上找到非常好的解决方案,虽然这些解决方案并不一定对应于全局最小值。
凸优化|Convex Optimization
使用数学方法(例如梯度下降法)寻找凸函数最小值的过程。机器学习方面的大量研究都是专注于如何通过公式将各种问题表示成凸优化问题,以及如何更高效地解决这些问题。
X
学习率|Learning Rate
在训练模型时用于梯度下降的一个变量。在每次迭代期间,梯度下降法都会将学习速率与梯度相乘。得出的乘积称为梯度步长。
学习速率是一个重要的超参数。
稀疏特征|Sparse Feature
一种特征向量,其中的大多数值都为 0 或为空。例如,某个向量包含一个为 1 的值和一百万个为 0 的值,则该向量就属于稀疏向量。再举一个例子,搜索查询中的单词也可能属于稀疏特征 - 在某种指定语言中有很多可能的单词,但在某个指定的查询中仅包含其中几个。
与密集特征相对。
协同过滤|Collabroative Filtering
根据很多其他用户的兴趣来预测某位用户的兴趣。协同过滤通常用在推荐系统中。
Y
预训练模型
已经过训练的模型或模型组件(例如嵌套)。有时,您需要将预训练的嵌套馈送到神经网络。在其他时候,您的模型将自行训练嵌套,而不依赖于预训练的嵌套。
Z
准确率|Accuracy
分类模型的正确预测所占的比例。在多类别分类中,准确率的定义如下:
$$ 准确率 = \frac { 正确预测数 } { 样本总数 } $$
在二元分类中,准确率的定义如下:
$$ 准确率 = \frac { 真正例数 + 真负例数 } { 样本总数 } $$
真负例
被模型正确地预测为负类别的样本。例如,模型推断出某封电子邮件不是垃圾邮件,而该电子邮件确实不是垃圾邮件。
真正例
被模型正确地预测为正类别的样本。例如,模型推断出某封电子邮件是垃圾邮件,而该电子邮件确实是垃圾邮件。
召回率
一种分类模型指标,用于回答以下问题:在所有可能的正类别标签中,模型正确地识别出了多少个?即:
$$ 召回率 = \frac { 真正例数 } { 真正例数 + 假正例数} $$
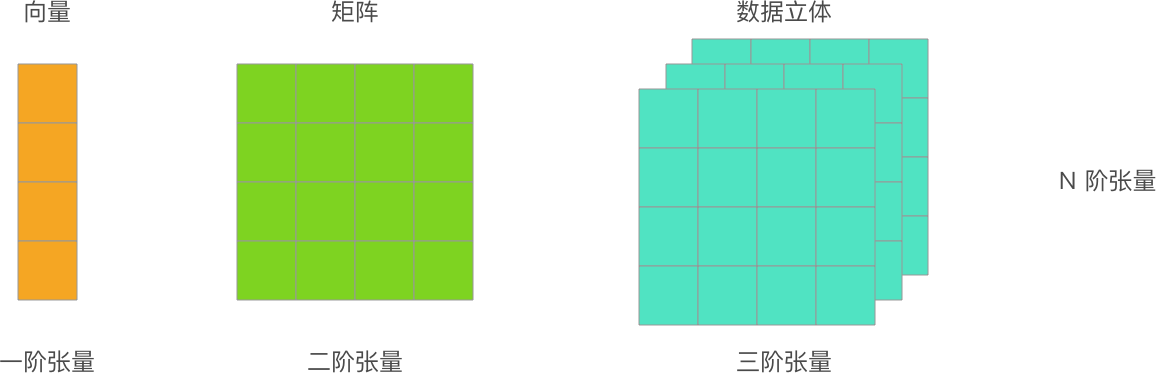
张量|Tensor
TensorFlow 程序中的主要数据结构。张量是 N 维(其中 N 可能非常大)数据结构,最常见的是标量、向量或矩阵。张量的元素可以包含整数值、浮点值或字符串值。
迁移学习|Transfer Learning
将信息从一个机器学习任务转移到另一个机器学习任务。例如,在多任务学习中,一个模型可以完成多项任务,例如针对不同任务具有不同输出节点的深度模型。迁移学习可能涉及将知识从较简单任务的解决方案转移到较复杂的任务,或者将知识从数据较多的任务转移到数据较少的任务。
大多数机器学习系统都只能完成一项任务。迁移学习是迈向人工智能的一小步;在人工智能中,单个程序可以完成多项任务。
L1 正则化|L1 Regularization
一种正则化,根据权重的绝对值的总和来惩罚权重。在依赖稀疏特征的模型中,L1 正则化有助于使不相关或几乎不相关的特征的权重正好为 0,从而将这些特征从模型中移除。与 L2 正则化相对。
L2 正则化|L2 Regularization
一种正则化,根据权重的平方和来惩罚权重。L2 正则化有助于使离群值(具有较大正值或较小负值)权重接近于 0,但又不正好为 0。(与 L1 正则化相对。)在线性模型中,L2 正则化始终可以改进泛化。
周期|Epoch
在训练时,整个数据集的一次完整遍历,以便不漏掉任何一个样本。因此,一个周期表示(N/批次规模)次训练迭代,其中 N 是样本总数。







