2018-11-30发表2020-10-23更新算法 / 排序算法9 分钟读完 (大约1285个字)0次访问

【排序算法】—— 更快的排序

在上篇【Python 排序算法】—— 基本排序算法中，介绍的 3 中排序算法都拥有 $O(n^2)$ 的运行时间。这些排序算法还有几种变体，其中的稍微快一些。但是，在最坏的情况和平均情况下，它们的性能还是 $O(n^2)$。然而，我们可以利用一些复杂度为 $O(nlogn)$ 的更好的算法。这些更好的算法的秘诀就是，采用分而治之$(divide-and-conquer)$的策略。也就是说，每一个算法都找了一种方法，将列表分解为更小的子列表。随后，这些子列表在递归地排序。理想情况下，如果这些子列表的复杂度为 $log(n)$，而重新排列每一个子列表中的数据所需的工作量为 $n$，那么，这样的排序算法总的复杂度就是 $O(nlogn)$。

这里将介绍两种排序算法，他们都突破了 $n^2$ 复杂度的障碍，它们是快速排序和合并排序。

快速排序简介

快速排序所使用的策略可以概括如下：

首先，从列表的中点位置选取一项。这一项叫做基准点$(pivot)$。
将列表中的项分区，以便小于基准点的所有项都移动到基准点的左边，而剩下的项都移动到基准点的右边。根据相关的实际项，基准点自身的最终位置也是变化的。例如，如果基准点自身是最大的项，它会位于列表的最右边，如果基准点是最小值，它会位于最左边。但是，不管基准点最终位于何处，这个位置都是它在完全排序的列表中的最终位置。
分而治之。对于在基准点分割列表而形成的子列表，递归地重复应用该过程。一个子列表包含了基准点左边的所有的项（现在是最小的项），另一个子列表包含了基准点右边的所有的项（现在是较大的项）。
每次遇到少于2个项的一个子列表，就结束这个过程。

分割

该算法最复杂的部分就是对子列表中的项进行分割的操作。有两种主要的方式用来进行分割。有一种方法较为容易，如何对任何子列表应用该方法的步骤如下：

将基准点和子列表的最后一项交换。
在已知小于基准点的项和剩余的项之间建立一个边界。一开始，这个边界就放在第 1 个项之前。
从子列表中的第 1 项开始，扫描整个子列表。每次遇到小于基准点的项，就将其与边界之后的第 1 项交换，且边界向后移动。
将基准点和边界之后的第 1 项交换，从而完成这个过程。

下图说明了对于数字12, 19, 17, 18, 14, 11, 15, 13 和 16 应用这些步骤的过程。在第 1 步中，建立了基准点并且将其与最后一项交换。在第 2 步中，在第 1 项之前建立了边界。在第 3 步到第 6 步，扫描了子列表以找到比基准点小的项，这些项将要和边界之后的第 1 项交换，并且边界向后移动。注意，边界左边的项总是小于基准点。最后，在第 7 步中，基准点和边界之后的第 1 项交换，子列表已经成功第分割好了。

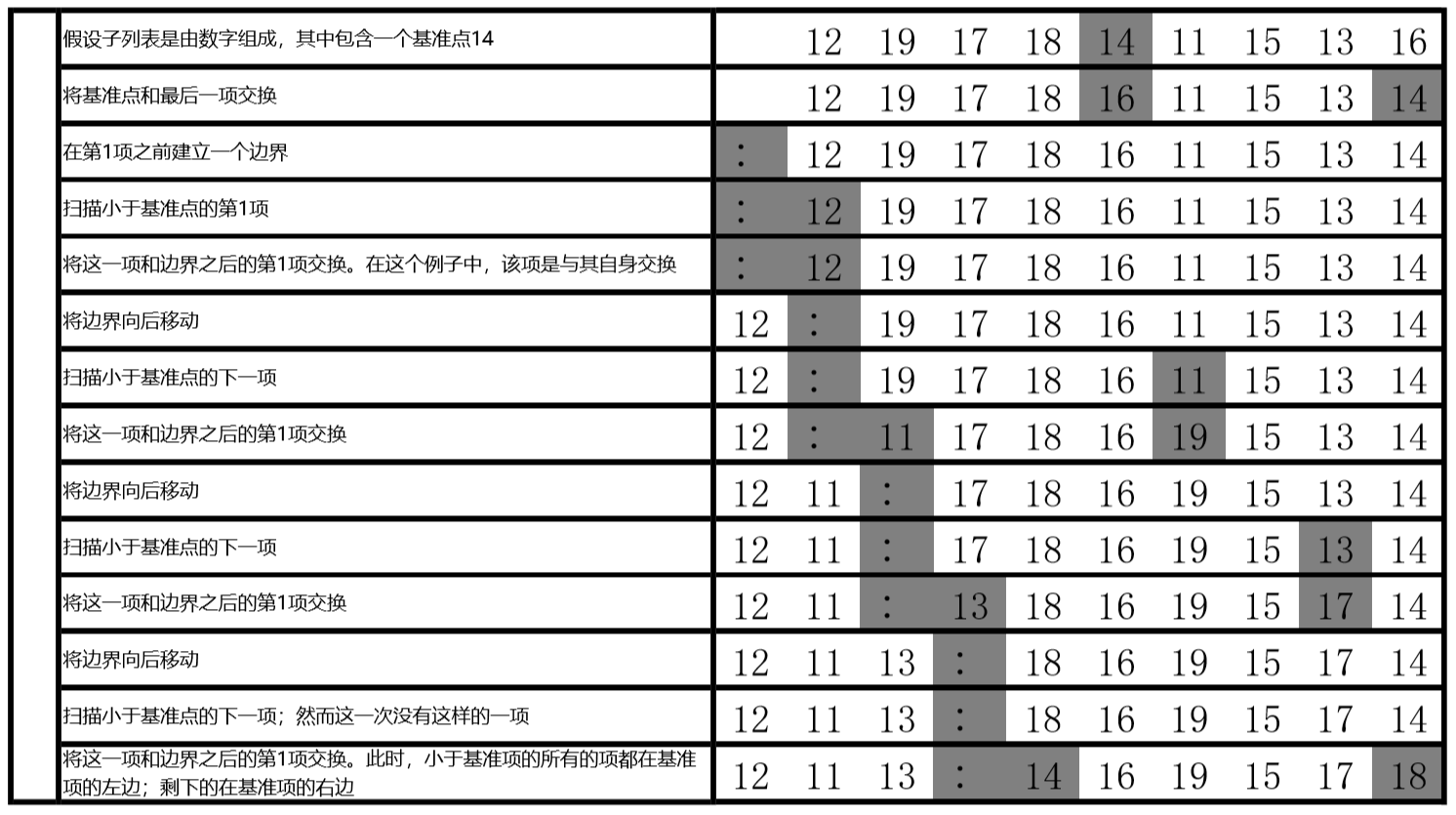
在分割好一个子列表之后，对于左边和右边的子列表（12，11，13 和 16，19，15，17，18）重复应用这个过程，直到子列表的长度最大为 1。

快速排序的实现

快速排序使用递归算法更容易编码。如下脚本定义了一个顶层的quicksort 函数；一个递归的quicksortHelper函数，它隐藏了用与子列表终点的额外参数；还有一个partition函数。如下脚本实在20个随机排序的整数组成的一个列表上执行快速排序。

def quicksort(lyst):
    quicksortHelper(lyst, 0, len(lyst) - 1)
    
def quicksortHelper(lyst, left, right):
    if left < right:
        pivotLocation = partition(lyst, left, right)
        quicksortHelper(lyst, left, pivotLocation - 1)
        quicksortHelper(lyst, pivotLocation + 1, right)
        
def partition(lyst, left, right):
    # Find the pivot and exchange it with the last item
    middle = (left + right) // 2
    pivot = lyst[middle]
    lyst[middle] = lyst[right]
    lyst[right] = pivot
    # Set boundary point to first position
    boundary = left
    # Move items less than pivot to the left
    for index in range(left, right):
        if lyst[index] < pivot:
            swap(lyst, index, boundary)
            boundary += 1
    # Exchange the pivot item and the boundary item
    swap(lyst, right, boundary)
    return boundary

# Earlier definition of the swap function goes here

import random

def main(size = 20, sort = quicksort):
    lyst = []
    for count in range(size):
        lyst.append(random.randint(1, size + 1))
    print(lyst)
    sort(lyst)
    print(lyst)
        
if __name__ == "__main__":
    main()