机器学习|线性回归算法详解
线性回归
线性回归是一种较为简单,但十分重要的机器学习方法。掌握线性的原理及求解方法,是深入了解线性回归的基本要求。除此之外,线性回归也是监督学习回归部分的基石。
线性回归介绍
在了解线性回归之前,我们得先了解分类和回归问题的区别。
首先,回归问题和分类问题一样,训练数据都包含标签,这也是监督学习的特点。而不同之处在于,分类问题预测的是类别,回归问题预测的是连续值。
例如,回归问题往往解决:
- 股票价格预测
- 房价预测
- 洪水水位线
上面列举的问题,我们需要预测的目标都不是类别,而是实数连续值。
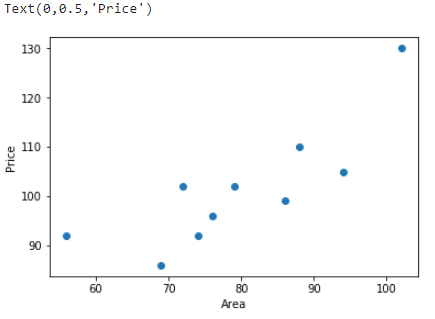
也就是说,回归问题旨在实现对连续值的预测,例如股票的价格、房价的趋势等。比如,下方展现了一个房屋面积和价格的对应关系图。
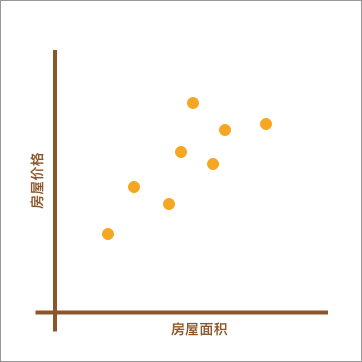
如上图所示,不同的房屋面积对应着不同的价格。现在,假设我手中有一套房屋想要出售,而出售时就需要预先对房屋进行估值。于是,我想通过上图,也就是其他房屋的售价来判断手中的房产价值是多少。应该怎么做呢?
我采用的方法是这样的。如下图所示,首先画了一条红色的直线,让其大致验证橙色点分布的延伸趋势。然后,我将已知房屋的面积大小对应到红色直线上,也就是蓝色点所在位置。最后,再找到蓝色点对应于房屋的价格作为房屋最终的预估价值。
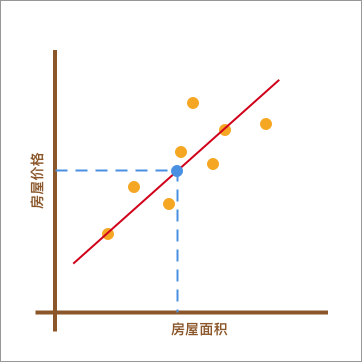
在上图呈现的这个过程中,通过找到一条直线去拟合数据点的分布趋势的过程,就是线性回归的过程。而线性回归中的「线性」代指线性关系,也就是图中所绘制的红色直线。
此时,你可能心中会有一个疑问。上图中的红色直线是怎么绘制出来的呢?为什么不可以像下图中另外两条绿色虚线,而偏偏要选择红色直线呢?
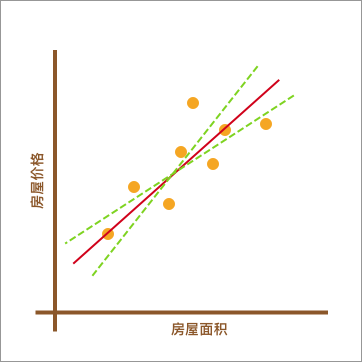
上图中的绿色虚线的确也能反应数据点的分布趋势。所以,找到最适合的那一条红色直线,也是线性回归中需要解决的重要问题之一。
通过上面这个小例子,相信你对线性回归已经有一点点印象了,至少大致明白它能做什么。接下来的内容中,我们将了解线性回归背后的数学原理,以及使用 Python 代码对其实现。
线性回归原理及实现
一元线性回归
上面针对线性回归的介绍内容中,我们列举了一个房屋面积与房价变化的例子。其中,房屋面积为自变量,而房价则为因变量。另外,我们将只有 1 个自变量的线性拟合过程叫做一元线性回归。
下面,我们就生成一组房屋面积和房价变化的示例数据。x 为房屋面积,单位是平方米; y 为房价,单位是万元。
1 | import numpy as np |
示例数据由 10 组房屋面积及价格对应组成。接下来,通过 Matplotlib 绘制数据点,x, y 分别对应着横坐标和纵坐标。
1 | from matplotlib import pyplot as plt |
正如上面所说,线性回归即通过线性方程(1 次函数)去拟合数据点。那么,我们令函数的表达式为:
$$ y(x, w) = w_0 + w_1x \tag{1} $$
公式(1)是典型的一元一次函数表达式,我们通过组合不同的 $w_0$ 和 $w_1$ 的值得到不同的拟合直线。我们对公式(1)进行代码实现:
1 | def f(x, w0, w1): |
那么,哪一条直线最能反应出数据的变化趋势呢?
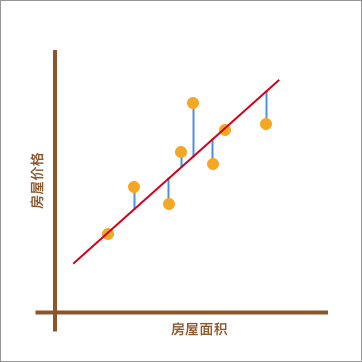
如下图所示,当我们使用 $y(x, w) = w_0 + w_1x$ 对数据进行拟合时,我们能得到拟合的整体误差,即图中蓝色线段的长度总和。如果某一条直线对应的误差值最小,是不是就代表这条直线最能反映数据点的分布趋势呢?
平方损失函数
正如上面所说,如果一个数据点为 ($x_{i}$, $y_{i}$),那么它对应的误差就为:
$$y_{i}-(w_0 + w_1x_{i}) \tag2$$
上面的误差往往也称之为残差。但是在机器学习中,我们更喜欢称作「损失」,即真实值和预测值之间的偏离程度。那么,对应 n 个全部数据点而言,其对应的残差损失总和就为:
$$
\sum\limits_{i = 1}^n (y_{i}-(w_0 + w_1x_{i})) \tag3
$$
在线性回归中,我们更偏向于使用均方误差作为衡量损失的指标,而均方误差即为残差的平方和。公式如下:
$$
\sum\limits_{i = 1}^n (y_{i}-(w_0 + w_1x_{i}))^2\tag4
$$
对于公式(4)而言,机器学习中有一个专门的名词,那就是「平方损失函数」。而为了得到拟合参数 $w_0$ 和 $w_1$ 最优的数值,我们的目标就是让公式(4)对应的平方损失函数最小。
同样,我们可以对公式(4)进行代码实现:
1 | def square_loss(x, y, w0, w1): |
最小二乘法及代数求解
最小二乘法是用于求解线性回归拟合参数 $w$ 的一种常用方法。最小二乘法中的「二乘」代表平方,最小二乘也就是最小平方。而这里的平方就是指代上面的平方损失函数。
简单来讲,最小二乘法也就是求解平方损失函数最小值的方法。那么,到底该怎样求解呢?这就需要使用到高等数学中的知识。推导如下:
首先,平方损失函数为:
$$
f = \sum\limits_{i = 1}^n (y_{i}-(w_0 + w_1x_{i}))^2 \tag5
$$
我们的目标是求取平方损失函数 $min(f)$ 最小时,对应的 $w$。首先求 $f$ 的 1 阶偏导数:
$$
\frac{\partial f}{\partial w_{0}}=-2(\sum_{i=1}^{n}{y_i}-nw_{0}-w_{1}\sum_{i=1}^{n}{x_i})\
\frac{\partial f}{\partial w_{1}}=-2(\sum_{i=1}^{n}{x_iy_i}-w_{0}\sum_{i=1}^{n}{x_i}-w_{1}\sum_{i=1}^{n}{x_i}^2) \tag6
$$
然后,我们令 $\frac{\partial f}{\partial w_{0}}=0$ 以及 $\frac{\partial f}{\partial w_{1}}=0$,解得:
$$
w_{1}=\frac {n\sum_{}^{}{x_iy_i}-\sum_{}^{}{x_i}\sum_{}^{}{y_i}} {n\sum_{}^{}{x_i}^2-(\sum_{}^{}{x_i})^2}\
w_{0}=\frac {\sum_{}^{}{x_i}^2\sum_{}^{}{y_i}-\sum_{}^{}{x_i}\sum_{}^{}{x_iy_i}} {n\sum_{}^{}{x_i}^2-(\sum_{}^{}{x_i})^2}\tag7
$$
到目前为止,已经求出了平方损失函数最小时对应的 $w$ 参数值,这也就是最佳拟合直线。
线性回归 Python 实现
我们将公式(7)求解得到 $w$ 的过程进行代码实现:
1 | def w_calculator(x, y): |
于是,可以向函数 w_calculator(x, y) 中传入 x 和 y 得到 $w_0$ 和 $w_1$ 的值。
1 | w_calculator(x, y) |
1 | (41.33509168550616, 0.7545842753077117) |
当然,我们也可以求得此时对应的平方损失的值:
1 | w0 = w_calculator(x, y)[0] |
1 | 447.69153479025357 |
接下来,我们尝试将拟合得到的直线绘制到原图中:
1 | x_temp = np.linspace(50,120,100) # 绘制直线生成的临时点 |
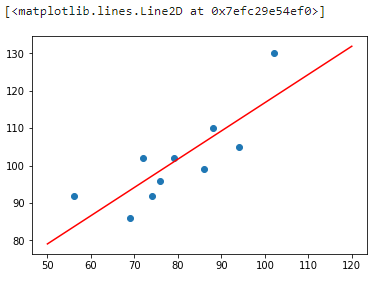
从上图可以看出,拟合的效果还是不错的。那么,如果你手中有一套 150 平米的房产想售卖,获得预估报价就只需要带入方程即可:
1 | f(150, w0, w1) |
1 | 154.5227329816629 |
这里得到的预估售价约为 154 万元。
线性回归 scikit-learn 实现
上面的内容中,我们学习了什么是最小二乘法,以及使用 Python 对最小二乘线性回归进行了完整实现。那么,我们如何利用机器学习开源模块 scikit-learn 实现最小二乘线性回归方法呢?
使用 scikit-learn 实现线性回归的过程会简单很多,这里要用到 LinearRegression() 类。看一下其中的参数:
1 | sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1) |
其中:
fit_intercept: 默认为 True,计算截距项。normalize: 默认为 False,不针对数据进行标准化处理。copy_X: 默认为 True,即使用数据的副本进行操作,防止影响原数据。n_jobs: 计算时的作业数量。默认为 1,若为 -1 则使用全部 CPU 参与运算。
1 | """scikit-learn 线性回归拟合 |
1 | (41.33509168550615, array([0.75458428])) |
我们通过 model.intercept_ 得到拟合的截距项,即上面的 $w_{0}$,通过 model.coef_ 得到 $x$ 的系数,即上面的 $w_{1}$。对比发现,结果是完全一致的。
同样,我们可以预测 150 平米房产的价格:
1 | model.predict([[150]]) |
1 | array([154.52273298]) |
可以看到,这里得出的结果和自行实现计算结果一致。
最小二乘法的矩阵推导及实现
学习完上面的内容,相信你已经了解了什么是最小二乘法,以及如何使用最小二乘法进行线性回归拟合。上面,实验采用了求偏导数的方法,并通过代数求解找到了最佳拟合参数 w 的值。
这里,我们尝试另外一种方法,即通过矩阵的变换来计算参数 w 。推导如下:
首先,一元线性函数的表达式为 $ y(x, w) = w_0 + w_1x$,表达成矩阵形式为:
$$\begin{bmatrix}1, x_{1} \ 1, x_{2} \ … \ 1, x_{9} \ 1, x_{10} \end{bmatrix} * \begin{bmatrix}w_{0} \ w_{1} \end{bmatrix} = \begin{bmatrix}y_{1} \ y_{2} \ … \ y_{9} \ y_{10} \end{bmatrix} \Rightarrow \begin{bmatrix}1, 56 \ 1, 72 \ … \ 1, 94 \ 1, 74 \end{bmatrix}* \begin{bmatrix}w_{0} \ w_{1} \end{bmatrix}= \begin{bmatrix}92 \ 102 \ … \ 105 \ 92 \end{bmatrix} \tag{8a}$$
即:
$$ y(x, w) = XW \tag{8b} $$
(8)式中,$W$ 为 $\begin{bmatrix}w_{0}
\ w_{1}
\end{bmatrix}$,而 $X$ 则是 $\begin{bmatrix}1, x_{1}
\ 1, x_{2}
\ …
\ 1, x_{9}
\ 1, x_{10}
\end{bmatrix}$ 矩阵。然后,平方损失函数为:
$$
f = \sum\limits_{i = 1}^n (y_{i}-(w_0 + w_1x_{i}))^2 =(y-XW)^T(y-XW)\tag{9}
$$
此时,对矩阵求偏导数(超纲)得到:
$$
\frac{\partial f}{\partial W}=2X^TXW-2X^Ty=0 \tag{10}
$$
当矩阵 $X^TX$ 满秩(不满秩后面的实验中会讨论)时,$(X^TX)^{-1}X^TX=E$,且 $EW=W$。所以,$(X^TX)^{-1}X^TXW=(X^TX)^{-1}X^Ty$。最终得到:
$$
W=(X^TX)^{-1}X^Ty \tag{11}
$$
我们可以针对公式(11)进行代码实现:
1 | def w_matrix(x, y): |
我们针对原 x 数据添加截距项系数 1。
1 | x = np.matrix([[1,56],[1,72],[1,69],[1,88],[1,102],[1,86],[1,76],[1,79],[1,94],[1,74]]) |
1 | matrix([[41.33509169], |
可以看到,矩阵计算结果和前面的代数计算结果一致。你可能会有疑问,那就是为什么要采用矩阵变换的方式计算?一开始学习的代数计算方法不好吗?
其实,并不是说代数计算方式不好,在小数据集下二者运算效率接近。但是,当我们面对十万或百万规模的数据时,矩阵计算的效率就会高很多,这就是为什么要学习矩阵计算的原因。
参考:







