机器学习| K-近邻算法详解
最近邻算法
介绍 K-近邻算法之前,首先说一说最近邻算法。最近邻算法(Nearest Neighbor,简称:NN),其针对未知类别数据 $x$,在训练集中找到与 $x$ 最相似的训练样本 $y$,用 $y$ 的样本对应的类别作为未知类别数据 $x$ 的类别,从而达到分类的效果。
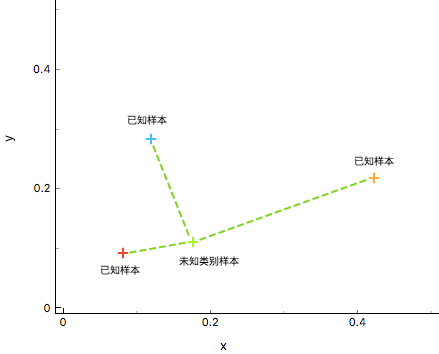
如上图所示,通过计算数据 $X_{u}$ (未知样本)和已知类别 ${\omega_{1},\omega_{2},\omega_{3}}$ (已知样本)之间的距离,判断 $X_{u}$ 与不同训练集的相似度,最终判断 $X_{u}$ 的类别。显然,这里将绿色未知样本类别判定与红色已知样本类别相同较为合适。
K-近邻算法
K-近邻(K-Nearest Neighbors,简称:KNN)算法是最近邻(NN)算法的一个推广,也是机器学习分类算法中最简单的方法之一。KNN 算法的核心思想和最近邻算法思想相似,都是通过寻找和未知样本相似的类别进行分类。但 NN 算法中只依赖 1 个样本进行决策,在分类时过于绝对,会造成分类效果差的情况,为解决 NN 算法的缺陷,KNN 算法采用 K 个相邻样本的方式共同决策未知样本的类别,这样在决策中容错率相对于 NN 算法就要高很多,分类效果也会更好。
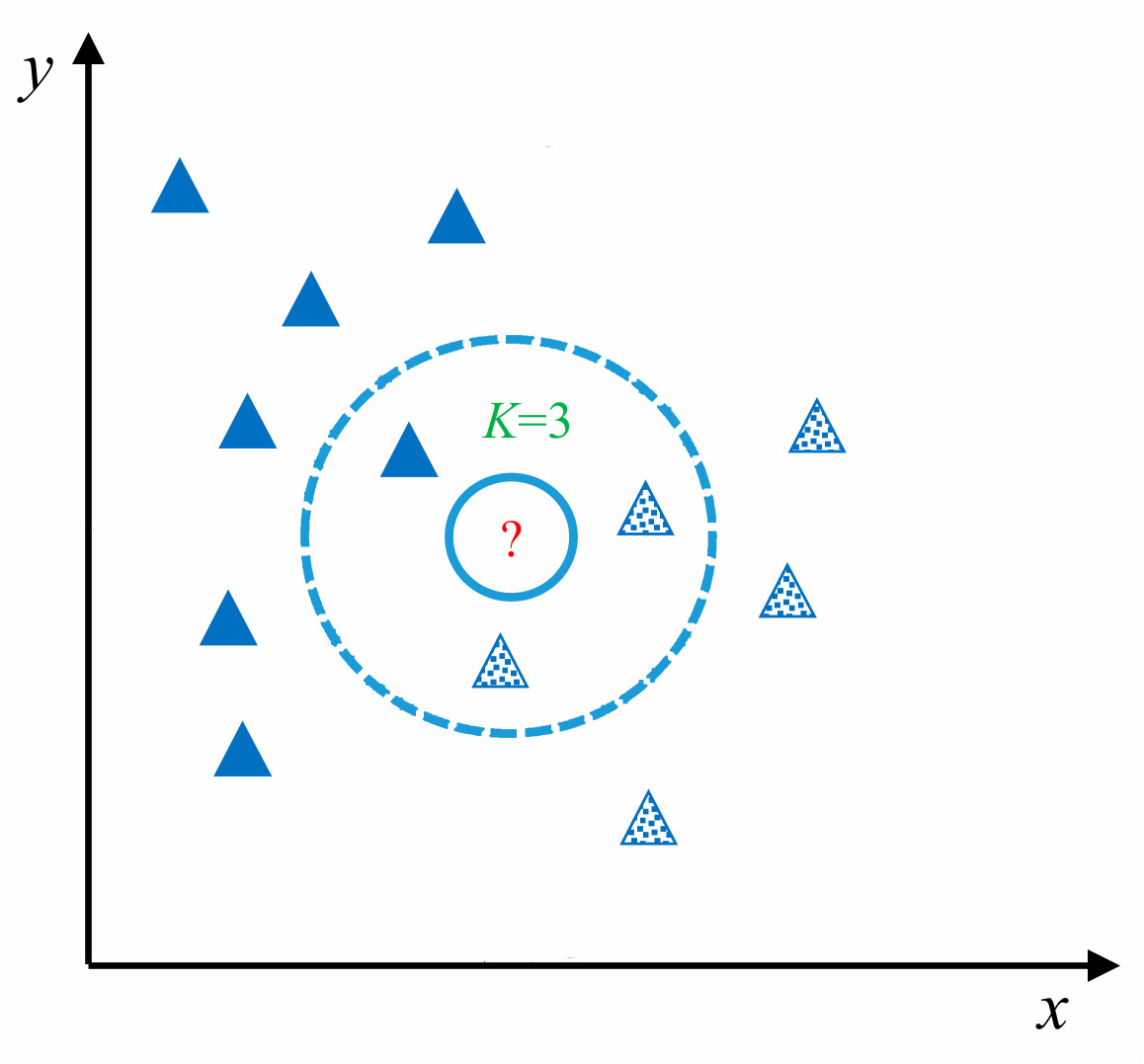
如上图所示,对于未知测试样本(图中 ?所示)采用 KNN 算法进行分类,首先计算未知样本和训练样本之间的相似度,找出最近 K 个相邻样本(在图中 K 值为 3,圈定距离 ?最近的 3 个样本),再根据最近的 K 个样本最终判断未知样本的类别。
K-近邻算法实现
KNN 算法在理论上已经非常成熟,其简单、易于理解的思想以及良好的分类准确度使得 KNN 算法应用非常广泛。算法的具体流程主要是以下的 4 个步骤:
- 数据准备:通过数据清洗,数据处理,将每条数据整理成向量。
- 计算距离:计算测试数据与训练数据之间的距离。
- 寻找邻居:找到与测试数据距离最近的 K 个训练数据样本。
- 决策分类:根据决策规则,从 K 个邻居得到测试数据的类别。

数据生成
下面,我们尝试完成一个 KNN 分类流程。首先,生成一组示例数据,共包含 2 个类别(A和B),其中每一条数据包含两个特征(x和y)。
1 | """生成示例数据 |
然后,我们尝试加载并打印这些数据。
1 | """打印示例数据 |
1 | features: |
为了更直观地理解数据,接下来用 Matplotlib 下的 pyplot 包来对数据集进行可视化。为了代码的简洁,我们使用了 map 函数和 lamda 表达式对数据进行处理。
1 | """示例数据绘图 |
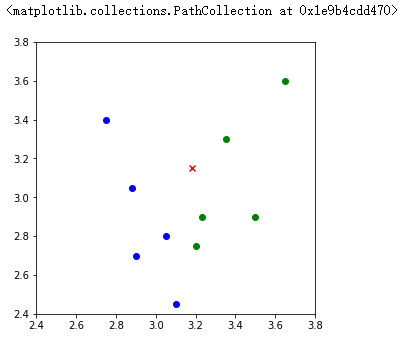
由上图所示,标签为 A(蓝色圆点)的数据在画布的左下角位置,而标签为 B(绿色圆点)的数据在画布的右上角位置,通过图像可以清楚看出不同标签数据的分布情况。其中红色 x 点即表示需预测类别的测试数据。
距离度量
在计算两个样本间的相似度时,可以通过计算样本之间特征值的距离进行表示。若两个样本距离值越大(相距越远),则表示两个样本相似度低,相反,若两个样本值越小(相距越近),则表示两个样本相似度越高。
计算距离的方法有很多,本实验介绍两个最为常用的距离公式:曼哈顿距离和欧式距离。这两个距离的计算图示如下:
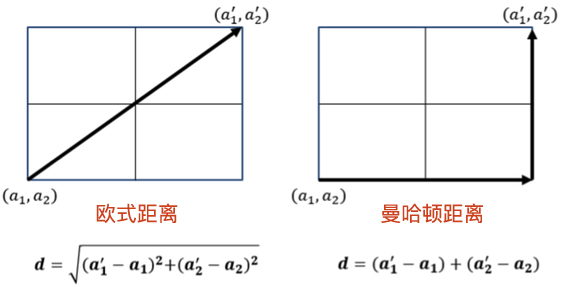
曼哈顿距离
曼哈顿距离又称马氏距离,出租车距离,是计算距离最简单的方式之一。公式如下:
$$
d_{man}=\sum_{i=1}^{N}\left | X_{i}-Y_{i} \right |
$$
其中:
- $X$,$Y$:两个数据点
- $N$:每个数据中有 $N$ 个特征值
- $X_{i}$ :数据 $X$ 的第 $i$ 个特征值
公式表示为将两个数据 $X$ 和 $Y$ 中每一个对应特征值之间差值的绝对值,再求和,便得到曼哈顿距离。
1 | """曼哈顿距离计算 |
1 | x: [3.1 3.2] |
欧式距离
欧式距离源自 $N$ 维欧氏空间中两点之间的距离公式。表达式如下:
$$
d_{euc}= \sqrt{\sum_{i=1}^{N}(X_{i}-Y_{i})^{2}}
$$
其中:
- $X$, $Y$ :两个数据点
- $N$:每个数据中有 $N$ 个特征值
- $X_{i}$ :数据 $X$ 的第 $i$ 个特征值
公式表示为将两个数据 X 和 Y 中的每一个对应特征值之间差值的平方,再求和,最后开平方,便是欧式距离。
1 | """欧氏距离的计算 |
1 | x: [0.10725148 0.78394185 0.85568109 0.5774587 0.96974919 0.79467734 |
决策规则
在得到测试样本和训练样本之间的相似度后,通过相似度的排名,可以得到每一个测试样本的 K 个相邻的训练样本,那如何通过 K 个邻居来判断测试样本的最终类别呢?可以根据数据特征对决策规则进行选取,不同的决策规则会产生不同的预测结果,最常用的决策规则是:
- 多数表决法:多数表决法类似于投票的过程,也就是在 K 个邻居中选择类别最多的种类作为测试样本的类别。
- 加权表决法:根据距离的远近,对近邻的投票进行加权,距离越近则权重越大,通过权重计算结果最大值的类为测试样本的类别。
这里推荐使用多数表决法,这种方法更加简单。
1 | """多数表决法 |
1 | [('C', 6), ('D', 5), ('A', 3), ('B', 2)] |
在多数表决法的定义中,我们导入了 operater 计算模块,目的是对字典类型结构排序。可以从结果中看出函数返回的结果为票数最多的 C,得票为 6 次。
KNN 算法实现
在学习完以上的各个步骤之后,KNN 算法也逐渐被勾勒出来。以下就是对 KNN 算法的完整实现,本次的距离计算采用欧式距离,分类的决策规则为多数表决法,定义函数 knn_classify(),其中函数的参数包括:
test_data:用于分类的输入向量。train_data:输入的训练样本集。labels:样本数据的类标签向量。k:用于选择最近邻居的数目。
1 | """KNN 方法完整实现 |
分类预测
在实现 KNN 算法之后,接下来就可以对我们未知数据[3.18,3.15]开始分类,假定我们 K 值初始设定为 5,让我们看看分类的效果。
1 | test_data = np.array([3.18, 3.15]) |
1 | [('B', 3), ('A', 2)] |
可视化展示
在对数据 [3.18,3.15] 实现分类之后,接下来我们同样用画图的方式形象化展示 KNN 算法决策方式。
1 | def circle(r, a, b): # 为了画出圆,这里采用极坐标的方式对圆进行表示 :x=r*cosθ,y=r*sinθ。 |
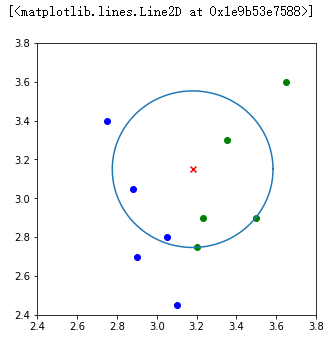
如图所示,当我们 K 值为 5 时,与测试样本距离最近的 5 个训练数据(如蓝色圆圈所示)中属于 B 类的有 3 个,属于 A 类的有 2 个,根据多数表决法决策出测试样本的数据为 B 类。
通过尝试不同的 K 值我们会发现,不同的 K 值预测出不同的结果。







