2019-01-19发表2020-10-23更新机器学习 / 朴素贝叶斯29 分钟读完 (大约4275个字)0次访问

机器学习| 朴素贝叶斯详解

在分类预测中，以概率论作为基础的算法比较少，而朴素贝叶斯就是其中之一。朴素贝叶斯算法实现简单，且预测分类的效率很高，是一种十分常用的算法。

朴素贝叶斯基础

基本概念

朴素贝叶斯的数学理论基础源于概率论。所以，在学习朴素贝叶斯算法之前，首先对其中涉及到的概率论知识做简要讲解。

条件概率

条件概率就是指事件 $A$ 在另外一个事件 $B$ 已经发生条件下的概率。如图所示：

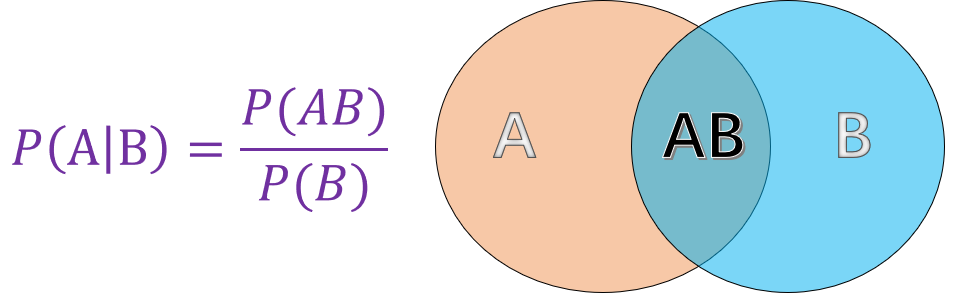
其中：

$P(A)$ 表示 $A$ 事件发生的概率。
$P(B)$ 表示 $B$ 事件发生的概率。
$P(AB)$ 表示 $A, B$ 事件同时发生的概率。

而最终计算得到的 $P(A \mid B)$ 便是条件概率，表示在 $B$ 事件发生的情况下 $A$ 事件发生的概率。

贝叶斯定理

上面提到了条件概率的基本概念，那么当知道事件 $B$ 发生的情况下事件 $A$ 发生的概率 $P(A \mid B)$，如何求 $P(B \mid A)$ 呢？贝叶斯定理应运而生。根据条件概率公式可以得到:

$$
P(B \mid A)=\frac{P(AB)}{P(A)} \tag1
$$
而同样通过条件概率公式可以得到：

$$
P(AB)=P(A \mid B)*P(B) \tag2
$$

将 (2) 式带入 (1) 式便可得到完整的贝叶斯定理：

$$
P(B \mid A)=\frac{P(AB)}{P(A)}=\frac{P(A \mid B)*P(B)}{P(A)} \tag{3}
$$
以下，通过一张图来完整且形象的展示条件概率和贝叶斯定理的原理。

先验概率

先验概率（Prior Probability）指的是根据以往经验和分析得到的概率。例如以上公式中的 $P(A), P(B)$,又例如：$X$ 表示投一枚质地均匀的硬币，正面朝上的概率，显然在我们根据以往的经验下，我们会认为 $X$ 的概率 $P(X) = 0.5$ 。其中 $P(X) = 0.5$ 就是先验概率。

后验概率

后验概率（Posterior Probability）是事件发生后求的反向条件概率；即基于先验概率通过贝叶斯公式求得的反向条件概率。例如公式中的 $P(B \mid A)$ 就是通过先验概率 $P(A)$和$P(B)$ 得到的后验概率，其通俗的讲就是「执果寻因」中的「因」。

什么是朴素贝叶斯

朴素贝叶斯（Naive Bayes）就是将贝叶斯原理以及条件独立结合而成的算法，其思想非常的简单，根据贝叶斯公式：
$$
P(B \mid A)=\frac{P(A \mid B)*P(B)}{P(A)} \tag{4}
$$
变形表达式为：
$$
P(类别 \mid 特征)=\frac{P(特征 \mid 类别) * P(类别)}{P(特征)} \tag{5}
$$
公式（5）利用先验概率，即特征和类别的概率；再利用不同类别中各个特征的概率分布，最后计算得到后验概率，即各个特征分布下的预测不同的类别。

利用贝叶斯原理求解固然是一个很好的方法，但实际生活中数据的特征之间是有相互联系的，在计算 $P(特征\mid类别)$ 时，考虑特征之间的联系会比较麻烦，而朴素贝叶斯则人为的将各个特征割裂开，认定特征之间相互独立。

朴素贝叶斯中的「朴素」，即条件独立，表示其假设预测的各个属性都是相互独立的,每个属性独立地对分类结果产生影响，条件独立在数学上的表示为：$P(AB)=P(A)*P(B)$。这样，使得朴素贝叶斯算法变得简单，但有时会牺牲一定的分类准确率。对于预测数据，求解在该预测数据的属性出现时各个类别的出现概率，将概率值大的类别作为预测数据的类别。

朴素贝叶斯算法实现

前面主要介绍了朴素贝叶斯算法中几个重要的概率论知识，接下来我们对其进行具体的实现，算法流程如下：

第 1 步：设
$$
X = \left { a_{1},a_{2},a_{3},…,a_{n} \right }
$$
为预测数据，其中 $a_{i}$ 是预测数据的特征值。

第 2 步：设
$$
Y = \left {y_{1},y_{2},y_{3},…,y_{m} \right }
$$
为类别集合。

第 3 步：计算 $P(y_{1}\mid x)$, $P(y_{2}\mid x)$, $P(y_{3}\mid x)$, $…$, $P(y_{m}\mid x)$。

第 4 步：寻找 $P(y_{1}\mid x)$, $P(y_{2}\mid x)$, $P(y_{3}\mid x)$, $…$, $P(y_{m}\mid x)$ 中最大的概率 $P(y_{k}\mid x)$ ，则 $x$ 属于类别 $y_{k}$。

生成示例数据

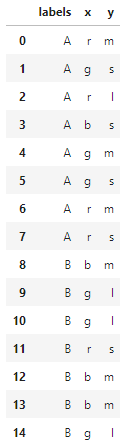
下面我们利用 python 完成一个朴素贝叶斯算法的分类。首先生成一组示例数据：由 A 和 B两个类别组成，每个类别包含 x,y两个特征值，其中 x 特征包含r,g,b（红，绿，蓝）三个类别，y特征包含s,m,l（小，中，大）三个类别，如同数据 $X = [g,l]$。

"""生成示例数据
"""
import pandas as pd


def create_data():
    data = {"x": ['r', 'g', 'r', 'b', 'g', 'g', 'r', 'r', 'b', 'g', 'g', 'r', 'b', 'b', 'g'],
            "y": ['m', 's', 'l', 's', 'm', 's', 'm', 's', 'm', 'l', 'l', 's', 'm', 'm', 'l'],
            "labels": ['A', 'A', 'A', 'A', 'A', 'A', 'A', 'A', 'B', 'B', 'B', 'B', 'B', 'B', 'B']}
    data = pd.DataFrame(data, columns=["labels", "x", "y"])
    return data

在创建好数据后，接下来进行加载数据，并进行预览。

"""加载并预览数据
"""
data = create_data()
data

参数估计

根据朴素贝叶斯的原理，最终分类的决策因素是比较 $\left { P(类别 1 \mid 特征),P(类别 2 \mid 特征),…,P(类别 m \mid 特征) \right }$ 各个概率的大小，根据贝叶斯公式得知每一个概率计算的分母 $P(特征)$ 都是相同的，只需要比较分子 $P(类别)$ 和 $P(特征 \mid 类别)$ 乘积的大小。

那么如何得到 $P(类别)$,以及 $P(特征\mid 类别)$呢？在概率论中，可以应用极大似然估计法以及贝叶斯估计法来估计相应的概率。

极大似然估计

什么是极大似然？下面通过一个简单的例子让你有一个形象的了解：

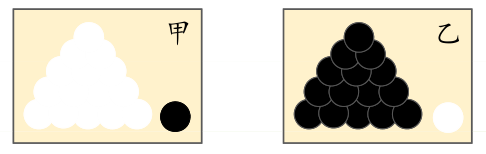
前提条件：假如有两个外形完全相同箱子，甲箱中有 99 个白球，1 个黑球；乙箱中有 99 个黑球，1 个白球。

问题：当我们进行一次实验，并取出一个球，取出的结果是白球。那么，请问白球是从哪一个箱子里取出的？

我相信，你的第一印象很可能会是白球从甲箱中取出。因为甲箱中的白球数量多，所以这个推断符合人们经验。其中「最可能」就是「极大似然」。而极大似然估计的目的就是利用已知样本结果，反推最有可能造成这个结果的参数值。

极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：「模型已定，参数未知」。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

在概率论中求解极大似然估计的方法比较复杂，基于实验，我们将讲解 $P(B)$ 和 $P(B/A)$ 是如何通过极大似然估计得到的。$P(种类)$ 用数学的方法表示：
$$
P(y_{i}=c_{k})=\frac{\sum_{N}^{i=1}I(y_{i}=c_{k})}{N},k=1,2,3,…,m \tag{6}
$$
公式(6)中的 $y_{i}$ 表示数据的类别，$c_{k}$ 表示每一条数据的类别。

你可以通俗的理解为，在现有的训练集中，每一个类别所占总数的比例，例如:生成的数据中 $P(Y=A)=\frac{8}{15}$，表示训练集中总共有 15 条数据，而类别为 A 的有 8 条数据。

下面我们用 Python 代码来实现先验概率 $P(种类)$ 的求解：

"""P(种类) 先验概率计算
"""


def get_P_labels(labels):
    labels = list(labels)  # 转换为 list 类型
    P_label = {}  # 设置空字典用于存入 label 的概率
    for label in labels:
        P_label[label] = labels.count(label) / float(len(labels))  # p = count(y) / count(Y)
    return P_label


P_labels = get_P_labels(data["labels"])
P_labels

1	{'A': 0.5333333333333333, 'B': 0.4666666666666667}

$P(特征 \mid 种类)$ 由于公式较为繁琐这里先不给出，直接用叙述的方式能更清晰地帮助理解：

实际需要求的先验估计是特征的每一个类别对应的每一个种类的概率，例如：生成数据 中 $P(x_{1}=”r” \mid Y=A)=\frac{4}{8}$， A 的数据有 8 条，而在种类为 A 的数据且特征 x 为 r的有 4 条。

同样我们用代码将先验概率 $P(特征 \mid 种类)$ 实现求解：

首先我们将特征按序号合并生成一个 numpy 类型的数组。

"""导入特征数据并预览
"""
import numpy as np

train_data = np.array(data.iloc[:, 1:])
train_data

array([['r', 'm'],
       ['g', 's'],
       ['r', 'l'],
       ['b', 's'],
       ['g', 'm'],
       ['g', 's'],
       ['r', 'm'],
       ['r', 's'],
       ['b', 'm'],
       ['g', 'l'],
       ['g', 'l'],
       ['r', 's'],
       ['b', 'm'],
       ['b', 'm'],
       ['g', 'l']], dtype=object)

在寻找属于某一类的某一个特征时，我们采用对比索引的方式来完成。
开始得到每一个类别的索引：

"""类别 A,B 索引
"""
labels = data["labels"]
label_index = []
for y in P_labels.keys():
    temp_index = []
    # enumerate 函数返回 Series 类型数的索引和值，其中 i 为索引，label 为值
    for i, label in enumerate(labels):
        if (label == y):
            temp_index.append(i)
        else:
            pass
    label_index.append(temp_index)
label_index

1	[[0, 1, 2, 3, 4, 5, 6, 7], [8, 9, 10, 11, 12, 13, 14]]

得到 A 和 B 的索引，其中是A类别为前 $8$ 条数据，B类别为后 $7$ 条数据。

在得到类别的索引之后，接下来就是找到我们需要的特征为 r的索引值。

"""特征 x 为 r 的索引
"""
x_index = [i for i, feature in enumerate(train_data[:, 0]) if feature == 'r']  # 效果等同于求类别索引中 for 循环
x_index

1	[0, 2, 6, 7, 11]

得到的结果为 $x$ 特征值为 $r$ 的数据索引值。

最后通过对比类别为 A 的索引值，计算出既符合 x = r 又符合 A 类别的数据在 A 类别中所占比例。

x_label = set(x_index) & set(label_index[0])
print('既符合 x = r 又是 A 类别的索引值：', x_label)
x_label_count = len(x_label)
print('先验概率 P(r|A):', x_label_count / float(len(label_index[0])))

1 2	既符合 x = r 又是 A 类别的索引值： {0, 2, 6, 7} 先验概率 P(r\|A): 0.5

为了方便后面函数调用，我们将求 $P(特征\mid 种类)$ 代码整合为一个函数。

"""P(特征∣种类) 先验概率计算
"""


def get_P_fea_lab(P_label, features, data):
    P_fea_lab = {}
    train_data = data.iloc[:, 1:]
    train_data = np.array(train_data)
    labels = data["labels"]
    for each_label in P_label.keys():
        label_index = [i for i, label in enumerate(
            labels) if label == each_label]  # labels 中出现 y 值的所有数值的下标索引
        # features[0] 在 trainData[:,0] 中出现的值的所有下标索引
        for j in range(len(features)):
            feature_index = [i for i, feature in enumerate(
                train_data[:, j]) if feature == features[j]]
            # set(x_index)&set(y_index) 列出两个表相同的元素
            fea_lab_count = len(set(feature_index) & set(label_index))
            key = str(features[j]) + '|' + str(each_label)
            P_fea_lab[key] = fea_lab_count / float(len(label_index))
    return P_fea_lab


features = ['r', 'm']
get_P_fea_lab(P_labels, features, data)

{'r|A': 0.5,
 'm|A': 0.375,
 'r|B': 0.14285714285714285,
 'm|B': 0.42857142857142855}

可以得到当特征 x 和 y 的值为 r 和 m 时，在不同类别下的先验概率。

贝叶斯估计

在做极大似然估计时，若类别中缺少一些特征，则就会出现概率值为 0 的情况。此时，就会影响后验概率的计算结果，使得分类产生偏差。而解决这一问题最好的方法就是采用贝叶斯估计。

在计算先验概率 $P(种类)$ 中，贝叶斯估计的数学表达式为：
$$
P(y_{i}=c_{k})=\frac{\sum_{N}^{i=1}I(y_{i}=c_{k})+\lambda }{N+k\lambda} \tag{8}
$$
其中 $\lambda \geq 0$ 等价于在随机变量各个取值的频数上赋予一个正数，当 $\lambda=0$ 时就是极大似然估计。在平时常取 $\lambda=1$，这时称为拉普拉斯平滑。例如：生成数据 中，$P(Y=A)=\frac{8+1}{15+2*1}=\frac{9}{17}$,取 $\lambda=1$ 此时由于一共有 A，B 两个类别，则 k 取 2。

同样计算 $P(特征 \mid 种类)$ 时，也是给计算时的分子分母加上拉普拉斯平滑。例如：生成数据 中，$P(x_{1}=”r” \mid Y=A)=\frac{4+1}{8+3*1}=\frac{5}{11}$ 同样取 $\lambda=1$ 此时由于 x 中有 r, g, b 三个种类，所以这里 k 取值为 3。

朴素贝叶斯算法实现

通过上面的内容，相信你已经对朴素贝叶斯算法原理有一定印象。接下来，我们对朴素贝叶斯分类过程进行完整实现。其中，参数估计方法则使用极大似然估计。
注：分类器实现的公式，请参考《机器学习》- 周志华 P151 页

"""朴素贝叶斯分类器
"""


def classify(data, features):
    # 求 labels 中每个 label 的先验概率
    labels = data['labels']
    P_label = get_P_labels(labels)
    P_fea_lab = get_P_fea_lab(P_label, features, data)

    P = {}
    P_show = {}  # 后验概率
    for each_label in P_label:
        P[each_label] = P_label[each_label]
        for each_feature in features:
            key = str(each_label)+'|'+str(features)
            P_show[key] = P[each_label] * \
                P_fea_lab[str(each_feature) + '|' + str(each_label)]
            P[each_label] = P[each_label] * \
                P_fea_lab[str(each_feature) + '|' +
                          str(each_label)]  # 由于分母相同，只需要比较分子
    print(P_show)
    features_label = max(P, key=P.get)  # 概率最大值对应的类别
    return features_label

1	classify(data, ['r', 'm'])

1 2	{"A\|['r', 'm']": 0.1, "B\|['r', 'm']": 0.02857142857142857} 'A'

对于特征为 [r,m] 的数据通过朴素贝叶斯分类得到不同类别的概率值，经过比较后分为 A 类。

朴素贝叶斯的三种常见模型

了解完朴素贝叶斯算法原理后，在实际数据中，我们可以依照特征的数据类型不同，在计算先验概率方面对朴素贝叶斯模型进行划分，并分为：多项式模型，伯努利模型和高斯模型。

多项式模型

当特征值为离散时，常常使用多项式模型。事实上，在以上实验的参数估计中，我们所应用的就是多项式模型。为避免概率值为 0 的情况出现，多项式模型采用的是贝叶斯估计。

伯努利模型

与多项式模型一样，伯努利模型适用于离散特征的情况，所不同的是，伯努利模型中每个特征的取值只能是 1 和 0（以文本分类为例，某个单词在文档中出现过，则其特征值为 1，否则为 0）。

在伯努利模型中，条件概率 $P(x_{i} \mid y_{k})$ 的计算方式为：

当特征值 $x_{i}=1$ 时，$P(x_{i} \mid y_{k})=P(x_{i}=1 \mid y_{k})$;
当特征值 $x_{i}=0$ 时，$P(x_{i} \mid y_{k})=P(x_{i}=0 \mid y_{k})$。

高斯模型

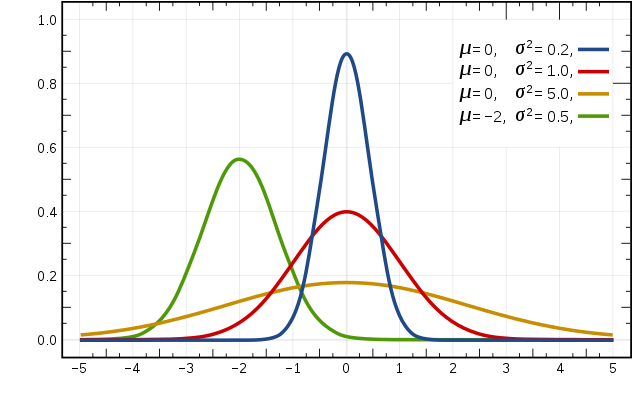
当特征是连续变量的时候，在不做平滑的情况下，运用多项式模型就会导致很多 $P(x_{i} \mid y_{k})=0$，此时即使做平滑，所得到的条件概率也难以描述真实情况。所以处理连续的特征变量，采用高斯模型。高斯模型是假设连续变量的特征数据是服从高斯分布的，高斯分布函数表达式为：
$$
P(x_{i}|y_{k})=\frac{1}{\sqrt{2\pi}\sigma_{y_{k},i}}exp(-\frac{(x-\mu_{y_{k},i}) ^{2}}{2\sigma ^{2}{y{k}},i})
$$
其中：