机器学习|决策树详解

决策树是一种特殊的树形结构，一般由节点和有向边组成。其中，节点表示特征、属性或者一个类，而有向边包含判断条件。决策树从根节点开始延伸，经过不同的判断条件后，到达不同的子节点。而上层子节点又可以作为父节点被进一步划分为下层子节点。一般情况下，我们从根节点输入数据，经过多次判断后，这些数据就会被分为不同的类别。这就构成了一颗简单的分类决策树。

举一个通俗的例子，假设在B站工作多年仍然单身的小B和他母亲在给他介绍对象时的一段对话：

母亲：小B，你都 28 了还是单身，明天亲戚家要来个姑娘要不要去见见。
小B：多大年纪？
母亲：26。
小B：有多高？
母亲：165厘米。
小B：长的好看不。
母亲：还行，比较朴素。
小B：温柔不？
母亲：看起来挺温柔的，很有礼貌。
小B：好，去见见。

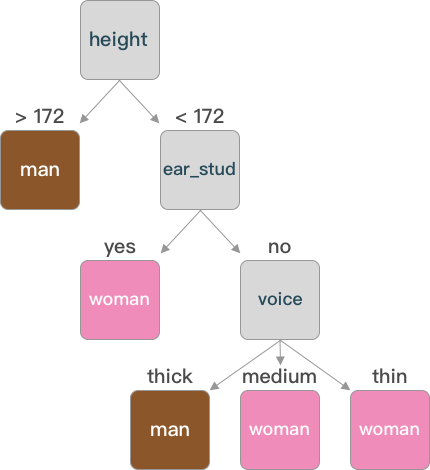
作为程序员的小B的思考逻辑就是典型的决策树分类逻辑，将年龄，身高，长相，是否温柔作为特征，并最后对见或者不见进行决策。其决策逻辑如图所示：

决策树算法实现

其实决策树算法如同上面场景一样，其思想非常容易理解，具体的算法流程为：

• 第 1 步: 数据准备：通过数据清洗和数据处理，将数据整理为没有缺省值的向量。
• 第 2 步: 寻找最佳特征：遍历每个特征的每一种划分方式，找到最好的划分特征。
• 第 3 步: 生成分支：划分成两个或多个节点。
• 第 4 步: 生成决策树：对分裂后的节点分别继续执行2-3步，直到每个节点只有一种类别。
• 第 5 步: 决策分类：根据训练决策树模型，将预测数据进行分类。

数据生成

下面我们依照决策树的算法流程，用 python 来实现决策树构建和分类。首先生成一组数据，数据包含两个类别 man 和 woman,特征分别为:

• hair:头发长短(long:长,short:短)
• voice:声音粗细(thick:粗,thin:细)
• height:身高
• ear_stud:是否带有耳钉(yes:是,no:没有)

|

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  
20  
21  
22  
23  
24  
25  
26  
27  
28  

|

"""生成示例数据  
"""  
import numpy as np  
import pandas as pd  
  
  
def create\_data():  
    data\_value = np.array(  
        \[\['long', 'thick', 175, 'no', 'man'\],  
         \['short', 'medium', 168, 'no', 'man'\],  
         \['short', 'thin', 178, 'yes', 'man'\],  
         \['short', 'thick', 172, 'no', 'man'\],  
         \['long', 'medium', 163, 'no', 'man'\],  
         \['short', 'thick', 180, 'no', 'man'\],  
         \['long', 'thick', 173, 'yes', 'man'\],  
         \['short', 'thin', 174, 'no', 'man'\],  
         \['long', 'thin', 164, 'yes', 'woman'\],  
         \['long', 'medium', 158, 'yes', 'woman'\],  
         \['long', 'thick', 161, 'yes', 'woman'\],  
         \['short', 'thin', 166, 'yes', 'woman'\],  
         \['long', 'thin', 158, 'no', 'woman'\],  
         \['short', 'medium', 163, 'no', 'woman'\],  
         \['long', 'thick', 161, 'yes', 'woman'\],  
         \['long', 'thin', 164, 'no', 'woman'\],  
         \['short', 'medium', 172, 'yes', 'woman'\]\])  
    columns = np.array(\['hair', 'voice', 'height', 'ear\_stud', 'labels'\])  
    data = pd.DataFrame(data\_value.reshape(17, 5), columns=columns)  
    return data  

|

在创建好数据之后，加载并打印出这些数据

|

1  
2  

|

data = create\_data()  
data  

|

划分选择

在得到数据后，根据算法流程，接下来需要寻找最优的划分特征，随着划分的不断进行，我们尽可能的将划分的分支所包含的样本归于同一类别，即结点的“纯度”越来越高。而常用的特征划分方式为信息增益和增益率。

信息增益（ID3）

在介绍信息增益之前，先引入“信息熵”的概念。“信息熵”是度量样本纯度最常用的一种指标，其公式为：

Ent(D)=−|y|∑k=1pklog2pk(1)

$$(1)Ent(D)=−∑k=1|y|pklog2pk$$

其中 D$D$ 表示样本集合，pk$pk$ 表示第 k$k$ 类样本所占的比例。其中 Ent(D)$Ent(D)$ 的值越小，则 D$D$ 的纯度越高。根据以上数据，在计算数据集的“信息熵”时，|y|$|y|$ 显然只有 man,woman 共 2 种，其中为 man 的概率为 817$817$, woman 的概率为 917$917$,则根据公式(1)得到数据集的纯度为：

Ent(data)=−2∑k=1pklog2pk=−(817log2817+917log2917)=0.9975

$$Ent(data)=−∑k=12pklog2pk=−(817log2817+917log2917)=0.9975$$

|

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  
20  
21  
22  
23  
24  
25  
26  
27  
28  
29  

|

"""计算信息熵  
"""  
import math  
  
  
def get\_Ent(data):  
    """  
    参数:  
    data -- 数据集  
  
    返回:  
    Ent -- 信息熵  
    """  
    num\_sample = len(data)  # 样本个数  
    label\_counts = {}  # 初始化标签统计字典  
    for i in range(num\_sample):  
        each\_data = data.iloc\[i, :\]  
        current\_label = each\_data\["labels"\]  # 得到当前元素的标签（label）  
  
        # 如果标签不在当前字典中，添加该类标签并初始化 value=0,否则该类标签 value+1  
        if current\_label not in label\_counts.keys():  
            label\_counts\[current\_label\] = 0  
        label\_counts\[current\_label\] += 1  
      
    Ent = 0.0  # 初始化信息熵  
    for key in label\_counts:  
        prob = float(label\_counts\[key\])/num\_sample  
        Ent -= prob \* math.log(prob, 2)  # 应用信息熵公式计算信息熵  
    return Ent  

|

通过计算信息熵函数，计算根节点的信息熵：

|

1  
2  

|

base\_ent = get\_Ent(data)  
base\_ent  

|

0.9975025463691153 

信息增益 就是建立在信息熵的基础上，在离散特征 x$x$ 有 M$M$ 个取值，如果用 x$x$ 对样本 D$D$ 来进行划分，就会产生 M$M$ 个分支，其中第 m$m$ 个分支包含了集合 D$D$ 的所有在特征 x$x$ 上取值为 m$m$ 的样本，记为 Dm$Dm$（例如：根据以上生成数据，如果我们用 hair 进行划分，则会产生long，short两个分支，每一个分支中分别包含了整个集合中属于 long 或者 short 的数据）。

考虑到不同分支节点包含样本数不同，给分支赋予权重 |Dm||D|$|Dm||D|$ ,使得样本越多的分支节点影响越大，则 信息增益 的公式就可以得到：

Gain(D,x)=Ent(D)−M∑m=1|Dm||D|Ent(Dm)(2)

$$(2)Gain(D,x)=Ent(D)−∑m=1M|Dm||D|Ent(Dm)$$

一般情况下，信息增益越大，则说明用 x$x$ 来划分样本集合 D$D$ 的纯度越高。以 hair 为例，其中它有 short 和 long 两个可能取值，则分别用 D1$D1$ (hair = long) 和 `D^{2} (hair = short)来表示。

其中为 D1$D1$ 的数据编号为 {0，4，6，8，9，10，12，14，15}${0，4，6，8，9，10，12，14，15}$ 共 9 个，在这之中为 man 的有 {0，4，6} 共3 个占比为39$39$，为 woman 的有{8, 9，10，12，14，15}共 6 个占比为69$69$; 同样 D2$D2$ 编号为{1，2，3，5，7，11，13, 16}共 8 个，其中为 man 的有{1，2，3，5，7}共 5 个占比58$58$,为 woman 的有{11，13, 16}共 3 个占比 38$38$,若按照 hair 进行划分，则两个分支点的信息熵为：

Ent(D1)=−(39log239+69log269)=0.449

$$Ent(D1)=−(39log239+69log269)=0.449$$

Ent(D2)=−(58log258+38log238)=0.486

$$Ent(D2)=−(58log258+38log238)=0.486$$

根据信息增益的公式可以计算出 hair 的信息增益为：

Gain(D,hair)=Ent(D)−2∑m=1|Dm||D|Ent(Dm)=0.9975−(917∗0.449+817∗0.486)=0.062

$$Gain(D,hair)=Ent(D)−∑m=12|Dm||D|Ent(Dm)=0.9975−(917∗0.449+817∗0.486)=0.062$$

下面我们用 python 来实现信息增益（ID3）算法：

|

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  
20  
21  
22  
23  
24  
25  
26  
27  

|

"""计算信息增益  
"""  
  
  
def get\_gain(data, base\_ent, feature):  
    """  
    参数:  
    data -- 数据集  
    base\_ent -- 根节点的信息熵  
    feature -- 计算信息增益的特征  
  
    返回:  
    Ent -- 信息熵  
    """  
  
    feature\_list = data\[feature\]  # 得到一个特征的全部取值  
    unique\_value = set(feature\_list)  # 特征取值的类别  
    feature\_ent = 0.0  
  
    for each\_feature in unique\_value:  
        temp\_data = data\[data\[feature\] == each\_feature\]  
        weight = len(temp\_data)/len(feature\_list)  # 计算该特征的权重值  
        temp\_ent = weight\*get\_Ent(temp\_data)  
        feature\_ent = feature\_ent+temp\_ent  
  
    gain = base\_ent - feature\_ent  # 信息增益  
    return gain  

|

完成 信息增益 函数后，尝试计算特征 hair 的信息增益值。

|

1  

|

get\_gain(data,base\_ent,'hair')  

|

0.062200515199107964 

信息增益率（C4.5）

信息增益也存在许多不足之处，经过大量的实验发现，当信息增益作为标准时，易偏向于取值较多的特征，为了避免这种偏好给预测结果带来的不好影响，可以使用增益率来选择最优划分。增益率的公式定义为:

GainRatio(D,a)=Gain(D,a)IV(a)(3)

$$(3)GainRatio(D,a)=Gain(D,a)IV(a)$$

其中：

IV(a)=−M∑m=1|Dm||D|log2|Dm||D|(4)

$$(4)IV(a)=−∑m=1M|Dm||D|log2|Dm||D|$$

IV(a)$IV(a)$ 称为特征 a$a$ 的固有值，当 a$a$ 的取值数目越多，则 IV(a)$IV(a)$ 的值通常会比较大。例如：

IV(hair)=−917log2917−817log2817=0.998

$$IV(hair)=−917log2917−817log2817=0.998$$

IV(voice)=−717log2717−517log2517−517log2517=1.566

$$IV(voice)=−717log2717−517log2517−517log2517=1.566$$

连续值处理

在前面介绍的特征选择中，都是对离散型数据进行处理，但在实际的生活中数据常常会出现连续值的情况，如生成数据中的身高，当数据较少时，可以将每一个值作为一个类别，但当数据量大时，这样是不可取的，在 C4.5 算法中采用二分法对连续值进行处理。

对于连续的属性 X$X$ 假设共出现了 n 个不同的取值，将这些取值从小到大排序{x1,x2,x3,…,xn}${x1,x2,x3,…,xn}$ ，其中找一点作为划分点 t ，则将数据划分为两类，大于 t 的为一类，小于 t 的为另一类。而 t 的取值通常为相邻两点的平均数 t=xi+xi+12$t=xi+xi+12$。

则在 n 个连续值之中，可以作为划分点的 t 有 n-1 个。通过遍历可以像离散型一样来考察这些划分点。

Gain(D,X)=Ent(D)−|D<t||D|Ent(D<t)−|D>t||D|Ent(D>t)(5)

$$(5)Gain(D,X)=Ent(D)−|D<t||D|Ent(D<t)−|D>t||D|Ent(D>t)$$

其中得到样本 D$D$ 基于划分点 t 二分后的信息增益，于是我们可以选择使得 Ga∈(D,X)$Ga∈(D,X)$ 值最大的划分点。

|

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  
20  
21  
22  
23  
24  
25  
26  
27  
28  
29  
30  
31  
32  
33  
34  
35  
36  
37  
38  
39  
40  

|

"""计算连续值的划分点  
"""  
  
  
def get\_splitpoint(data, base\_ent, feature):  
    """  
    参数:  
    data -- 数据集  
    base\_ent -- 根节点的信息熵  
    feature -- 需要划分的连续特征  
  
    返回:  
    final\_t -- 连续值最优划分点  
    """  
    # 将连续值进行排序并转化为浮点类型  
    continues\_value = data\[feature\].sort\_values().astype(np.float64)  
    continues\_value = \[i for i in continues\_value\]  # 不保留原来的索引  
    t\_set = \[\]  
    t\_ent = {}  
  
    # 得到划分点 t 的集合  
    for i in range(len(continues\_value)-1):  
        temp\_t = (continues\_value\[i\]+continues\_value\[i+1\])/2  
        t\_set.append(temp\_t)  
  
    # 计算最优划分点  
    for each\_t in t\_set:  
        # 将大于划分点的分为一类  
        temp1\_data = data\[data\[feature\].astype(np.float64) > each\_t\]  
        # 将小于划分点的分为一类  
        temp2\_data = data\[data\[feature\].astype(np.float64) < each\_t\]  
        weight1 = len(temp1\_data)/len(data)  
        weight2 = len(temp2\_data)/len(data)  
        # 计算每个划分点的信息增益  
        temp\_ent = base\_ent-weight1 \* \\  
            get\_Ent(temp1\_data)-weight2\*get\_Ent(temp2\_data)  
        t\_ent\[each\_t\] = temp\_ent  
    print("t\_ent:", t\_ent)  
    final\_t = max(t\_ent, key=t\_ent.get)  
    return final\_t  

|

实现连续值最优划分点的函数后，寻找 height 连续特征值的划分点。

|

1  
2  

|

final\_t = get\_splitpoint(data, base\_ent, 'height')  
final\_t  

|

t_ent: {158.0: 0.1179805181500242, 159.5: 0.1179805181500242, 161.0: 0.2624392604045631, 162.0: 0.2624392604045631, 163.0: 0.3856047022157598, 163.5: 0.15618502398692893, 164.0: 0.3635040117533678, 165.0: 0.33712865788827096, 167.0: 0.4752766311586692, 170.0: 0.32920899348970845, 172.0: 0.5728389611412551, 172.5: 0.4248356349861979, 173.5: 0.3165383509071513, 174.5: 0.22314940393447813, 176.5: 0.14078143361499595, 179.0: 0.06696192680347068}

172.0 

算法实现

在对决策树中最佳特征选择和连续值处理之后，接下来就是对决策树的构建。

数据预处理

首先我们将连续值进行处理，在找到最佳划分点之后，将 <t$<t$ 的值设为 0，将 >=t$>=t$ 的值设为 1。

|

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  

|

def choice\_1(x, t):  
    if x > t:  
        return ">{}".format(t)  
    else:  
        return "<{}".format(t)  
  
  
deal\_data = data.copy()  
\# 使用lambda和map函数将 height 按照final\_t划分为两个类别  
deal\_data\["height"\] = pd.Series(  
    map(lambda x: choice\_1(int(x), final\_t), deal\_data\["height"\]))  
deal\_data  

|

选择最优划分特征

将数据进行预处理之后，接下来就是选择最优的划分特征。

|

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  
20  
21  
22  

|

"""选择最优划分特征  
"""  
  
  
def choose\_feature(data):  
    """  
    参数:  
    data -- 数据集  
  
    返回:  
    best\_feature -- 最优的划分特征  
    """  
    num\_features = len(data.columns) - 1  # 特征数量  
    base\_ent = get\_Ent(data)  
    best\_gain = 0.0  # 初始化信息增益  
    best\_feature = data.columns\[0\]  
    for i in range(num\_features):  # 遍历所有特征  
        temp\_gain = get\_gain(data, base\_ent, data.columns\[i\])    # 计算信息增益  
        if (temp\_gain > best\_gain):  # 选择最大的信息增益  
            best\_gain = temp\_gain  
            best\_feature = data.columns\[i\]  
    return best\_feature  # 返回最优特征  

|

完成函数之后，我们首先看看数据集中信息增益值最大的特征是什么？

|

1  

|

choose\_feature(deal\_data)  

|

'height' 

构建决策树

在将所有的子模块构建好之后，最后就是对核心决策树的构建，本次实验采用信息增益（ID3）的方式构建决策树。在构建的过程中，根据算法流程，我们反复遍历数据集，计算每一个特征的信息增益，通过比较将最好的特征作为父节点，根据特征的值确定分支子节点，然后重复以上操作，直到某一个分支全部属于同一类别，或者遍历完所有的数据特征，当遍历到最后一个特征时，若分支数据依然“不纯”，就将其中数量较多的类别作为子节点。

因此最好采用递归的方式来构建决策树。

|

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  
20  
21  
22  
23  
24  
25  
26  
27  
28  
29  

|

"""构建决策树  
"""  
  
  
def create\_tree(data):  
    """  
    参数:  
    data -- 数据集  
  
    返回:  
    tree -- 以字典的形式返回决策树  
    """  
    feature\_list = data.columns\[:-1\].tolist()  
    label\_list = data.iloc\[:, -1\]  
    if len(data\["labels"\].value\_counts()) == 1:  
        leaf\_node = data\["labels"\].mode().values  
        return leaf\_node            # 第一个递归结束条件：所有的类标签完全相同  
    if len(feature\_list) == 1:  
        leaf\_node = data\["labels"\].mode().values  
        return leaf\_node   # 第二个递归结束条件：用完了所有特征  
    best\_feature = choose\_feature(data)   # 最优划分特征  
    tree = {best\_feature: {}}  
    feat\_values = data\[best\_feature\]  
    unique\_value = set(feat\_values)  
    for value in unique\_value:  
        temp\_data = data\[data\[best\_feature\] == value\]  
        temp\_data = temp\_data.drop(\[best\_feature\], axis=1)  
        tree\[best\_feature\]\[value\] = create\_tree(temp\_data)  
    return tree  

|

完成创建决策树函数后，接下来对我们第一棵树进行创建。

|

1  
2  

|

tree = create\_tree(deal\_data)  
tree  

|

{'height': {'<172.0': {'ear_stud': {'no': {'voice': {'thick': array(['man'], dtype=object),
      'medium': array(['man'], dtype=object),
      'thin': array(['woman'], dtype=object)}},
    'yes': array(['woman'], dtype=object)}},
  '>172.0': array(['man'], dtype=object)}} 

通过字典的方式表示构建好的树，可以通过图像的方式更加直观的了解。

通过图形可以看出，在构建决策树时不一定每一个特征都会成为树的节点（如同 hair）。

决策分类

在构建好决策树之后，最终就可以使用未知样本进行预测分类。

|

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  
20  
21  
22  
23  
24  

|

"""决策分类  
"""  
  
  
def classify(tree, test):  
    """  
    参数:  
    data -- 数据集  
    test -- 需要测试的数据  
  
    返回:  
    class\_label -- 分类结果  
    """  
    first\_feature = list(tree.keys())\[0\]  # 获取根节点  
    feature\_dict = tree\[first\_feature\]  # 根节点下的树  
    labels = test.columns.tolist()  
    value = test\[first\_feature\]\[0\]  
    for key in feature\_dict.keys():  
        if value == key:  
            if type(feature\_dict\[key\]).\_\_name\_\_ == 'dict':  # 判断该节点是否为叶节点  
                class\_label = classify(feature\_dict\[key\], test)  # 采用递归直到遍历到叶节点  
            else:  
                class\_label = feature\_dict\[key\]  
    return class\_label  

|

在分类函数完成之后，接下来我们尝试对未知数据进行分类。

|

1  
2  

|

test = pd.DataFrame({"hair": \["long"\], "voice": \["thin"\], "height": \[163\], "ear\_stud": \["yes"\]})  
test  

|

对连续值进行预处理。

|

1  
2  

|

test\["height"\] = pd.Series(map(lambda x: choice\_1(int(x), final\_t), test\["height"\]))  
test  

|

分类预测。

|

1  

|

classify(tree,test)  

|

array(['woman'], dtype=object) 

一个身高 163 厘米，长发，带着耳钉且声音纤细的人，在我们构建的决策树判断后预测为一名女性。

上面的实验中，我们没有考虑 =划分点 的情况，你可以自行尝试将 >=划分点 或 <=划分点 归为一类，看看结果又有哪些不同？

预剪枝和后剪枝

在决策树的构建过程中，特别在数据特征非常多时，为了尽可能正确的划分每一个训练样本，结点的划分就会不停的重复，则一棵决策树的分支就非常多。对于训练集而言，拟合出来的模型是非常完美的。但是，这种完美就使得整体模型的复杂度变高，同时对其他数据集的预测能力下降，也就是我们常说的过拟合使得模型的泛化能力变弱。为了避免过拟合问题的出现，在决策树中最常见的两种方法就是预剪枝和后剪枝。

预剪枝

预剪枝，顾名思义预先减去枝叶，在构建决策树模型的时候，每一次对数据划分之前进行估计，如果当前节点的划分不能带来决策树泛化的提升，则停止划分并将当前节点标记为叶节点。例如前面构造的决策树，按照决策树的构建原则，通过 height 特征进行划分后 <172 分支中又按照 ear_stud 特征值进行继续划分。如果应用预剪枝，则当通过 height 进行特征划分之后，对 <172 分支是否进行 ear_stud 特征进行划分时计算划分前后的准确度，如果划分后的更高则按照 ear_stud 继续划分，如果更低则停止划分。

后剪枝

跟预剪枝在构建决策树的过程中判断是否继续特征划分所不同的是，后剪枝在决策树构建好之后对树进行修剪。如果说预剪枝是自顶向下的修剪，那么后剪枝就是自底向上进行修剪。后剪枝将最后的分支节点替换为叶节点，判断是否带来决策树泛化的提升，是则进行修剪，并将该分支节点替换为叶节点，否则不进行修剪。例如在前面构建好决策树之后，>172分支的 voice 特征，将其替换为叶节点如（man），计算替换前后划分准确度，如果替换后准确度更高则进行修剪（用叶节点替换分支节点），否则不修剪。

预测分类

在前面我们使用 python 将决策树的特征选择，连续值处理和预测分类做了详细的讲解。接下来我们应用决策树模型对真实的数据进行分类预测。

导入数据

本次应用到的数据为学生成绩数据集 course-13-student.csv，一共有 395 条数据，26 个特征。

数据集下载 👉 传送门

|

1  
2  
3  
4  
5  
6  

|

"""导入数据集并预览  
"""  
import pandas as pd  
  
stu\_grade = pd.read\_csv('course-13-student.csv')  
stu\_grade.head()  

|

由于特征过多，我们选择部分特征作为决策树模型的分类特征,分别为：

• school：学生所读学校(GP，MS)
• sex: 性别(F：女，M：男)
• address: 家庭住址(U：城市，R：郊区)
• Pstatus: 父母状态(A：同居，T：分居)
• Pedu: 父母学历由低到高
• reason: 选择这所学校的原因(home：家庭,course：课程设计，reputation：学校地位，other：其他)
• guardian: 监护人(mother：母亲，father：父亲，other：其他)
• studytime: 周末学习时长
• schoolsup: 额外教育支持(yes：有，no：没有)
• famsup: 家庭教育支持(yes：有，no：没有)
• paid: 是否上补习班(yes：是，no：否)
• higher: 是否想受更好的教育(yes：是，no：否)
• internet: 是否家里联网(yes：是，no：否)
• G1: 一阶段测试成绩
• G2: 二阶段测试成绩
• G3: 最终成绩

|

1  
2  

|

new\_data = stu\_grade.iloc\[:, \[0, 1, 2, 3, 4, 5, 6, 8, 9, 10, 11, 14, 15, 24, 25, 26\]\]  
new\_data.head()  

|

数据预处理

首先我们将成绩 G1，G2，G3 根据分数进行等级划分，将 0-4 划分为 bad，5-9 划分为 medium ，

|

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  
17  

|

def choice\_2(x):  
    x = int(x)  
    if x < 5:  
        return "bad"  
    elif x >= 5 and x < 10:  
        return "medium"  
    elif x >= 10 and x < 15:  
        return "good"  
    else:  
        return "excellent"  
  
  
stu\_data = new\_data.copy()  
stu\_data\["G1"\] = pd.Series(map(lambda x: choice\_2(x), stu\_data\["G1"\]))  
stu\_data\["G2"\] = pd.Series(map(lambda x: choice\_2(x), stu\_data\["G2"\]))  
stu\_data\["G3"\] = pd.Series(map(lambda x: choice\_2(x), stu\_data\["G3"\]))  
stu\_data.head()  

|

同样我们对 Pedu （父母教育程度）也进行划分

|

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  

|

def choice\_3(x):  
    x = int(x)  
    if x > 3:  
        return "high"  
    elif x > 1.5:  
        return "medium"  
    else:  
        return "low"  
  
  
stu\_data\["Pedu"\] = pd.Series(map(lambda x: choice\_3(x), stu\_data\["Pedu"\]))  
stu\_data.head()  

|

在等级划分之后，为遵循 scikit-learn 函数的输入规范，需要将数据特征进行替换。

|

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  

|

"""特征值替换  
"""  
  
def replace\_feature(data):  
    """  
    参数:  
    data -- 数据集  
  
    返回:  
    data -- 将特征值替换后的数据集  
    """  
    for each in data.columns:  # 遍历每一个特征名称  
        feature\_list = data\[each\]  
        unique\_value = set(feature\_list)  
        i = 0  
        for fea\_value in unique\_value:  
            data\[each\] = data\[each\].replace(fea\_value, i)  
            i += 1  
    return data  

|

将特征值进行替换后展示。

|

1  
2  

|

stu\_data = replace\_feature(stu\_data)  
stu\_data.head(10)  

|

数据划分

加载好预处理的数据集之后，为了实现决策树算法，同样我们需要将数据集分为 训练集和测试集，依照经验：训练集占比为 70%，测试集占 30%。

同样在此我们使用 scikit-learn 模块的 train_test_split 函数完成数据集切分。

|

1  
2  
3  

|

from sklearn.model\_selection import train\_test\_split  
  
x\_train,x\_test, y\_train, y\_test =train\_test\_split(train\_data,train\_target,test\_size=0.4, random\_state=0)  

|

其中：

• x_train,x_test, y_train, y_test 分别表示，切分后的 特征的训练集，特征的测试集，标签的训练集，标签的测试集；其中特征和标签的值是一一对应的。
• train_data,train_target分别表示为待划分的特征集和待划分的标签集。
• test_size：测试样本所占比例。
• random_state：随机数种子,在需要重复实验时，保证在随机数种子一样时能得到一组一样的随机数。

|

1  
2  
3  
4  
5  
6  

|

from sklearn.model\_selection import train\_test\_split  
  
x\_train, x\_test, y\_train, y\_test = train\_test\_split(stu\_data.iloc\[:, :-1\], stu\_data\["G3"\],   
                                                    test\_size=0.3, random\_state=5)  
  
x\_test  

|

决策树构建

在划分好数据集之后，接下来就是进行预测。在前面的实验中我们采用 python 对决策树算法进行实现，下面我们通过 scikit-learn 来对其进行实现。 scikit-learn 决策树类及常用参数如下：

|

1  

|

DecisionTreeClassifier(criterion=’gini’，random\_state=None)  

|

其中：

• criterion 表示特征划分方法选择，默认为 gini (在后面会讲到)，可选择为 entropy (信息增益)。
• ramdom_state 表示随机数种子，当特征特别多时 scikit-learn 为了提高效率，随机选取部分特征来进行特征选择，即找到所有特征中较优的特征。

常用方法:

• fit(x,y)训练决策树。
• predict(X) 对数据集进行预测返回预测结果。

|

1  
2  
3  
4  

|

from sklearn.tree import DecisionTreeClassifier  
  
dt\_model = DecisionTreeClassifier(criterion='entropy', random\_state=34)  
dt\_model.fit(x\_train,y\_train) # 使用训练集训练模型  

|

DecisionTreeClassifier(class_weight=None, criterion='entropy', max_depth=None,
            max_features=None, max_leaf_nodes=None,
            min_impurity_decrease=0.0, min_impurity_split=None,
            min_samples_leaf=1, min_samples_split=2,
            min_weight_fraction_leaf=0.0, presort=False, random_state=34,
            splitter='best') 

决策树可视化

在构建好决策树之后，我们需要对创建好的决策树进行可视化展示，引入 export_graphviz 进行画图。由于环境中没有函数需要进行安装。

|

1  
2  
3  
4  
5  
6  

|

\# Linux  
!apt-get install --yes graphviz # 安装所需模块  
!pip install graphviz  
  
\# windows Anaconda  
conda install graphviz  

|

下面开始生成决策树图像，其中生成决策树较大需要拖动滑动条进行查看。

|

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  

|

from sklearn.tree import export\_graphviz  
import graphviz  
  
img = export\_graphviz(  
    dt\_model, out\_file=None,  
    feature\_names=stu\_data.columns\[:-1\].values.tolist(),  # 传入特征名称  
    class\_names=np.array(\["bad", "medium", "good", "excellent"\]),  # 传入类别值  
    filled=True, node\_ids=True,  
    rounded=True)  
  
graphviz.Source(img)  # 展示决策树  

|

svg

模型预测

|

1  
2  

|

y\_predict = dt\_model.predict(x\_test) # 使用模型对测试集进行预测  
y\_predict  

|

array([3, 1, 2, 0, 0, 2, 0, 2, 2, 2, 2, 0, 2, 3, 0, 3, 2, 0, 3, 2, 2, 0,
       3, 2, 2, 0, 3, 3, 2, 2, 0, 0, 0, 2, 1, 0, 1, 2, 3, 0, 3, 3, 2, 2,
       0, 2, 2, 2, 2, 2, 3, 2, 2, 0, 3, 0, 2, 2, 2, 1, 3, 0, 2, 2, 2, 2,
       3, 3, 2, 0, 0, 0, 1, 2, 2, 0, 0, 3, 0, 3, 2, 3, 2, 2, 3, 1, 0, 0,
       0, 2, 1, 2, 2, 2, 2, 3, 0, 0, 3, 0, 0, 2, 3, 2, 1, 2, 2, 0, 0, 2,
       0, 2, 0, 3, 2, 2, 2, 3, 2], dtype=int64) 

分类准确率计算

当我们训练好模型并进行分类预测之后，可以通过比对预测结果和真实结果得到预测的准确率。

accur=∑Ni=1I(¯yi=yi)N(6)

$$(6)accur=∑i=1NI(yi¯=yi)N$$

公式(6)中 N$N$ 表示数据总条数，¯yi$yi¯$ 表示第 i$i$ 条数据的种类预测值，yi$yi$ 表示第 i$i$ 条数据的种类真实值，I$I$ 同样是指示函数，表示 ¯yi$yi¯$ 和 yi$yi$ 相同的个数。

|

1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  

|

"""准确率计算  
"""  
  
def get\_accuracy(test\_labels, pred\_labels):  
    """  
    参数:  
    test\_labels -- 测试集的真实值  
    pred\_labels -- 测试集的预测值  
  
    返回:  
    accur -- 准确率  
    """  
    correct = np.sum(test\_labels == pred\_labels)  # 计算预测正确的数据个数  
    n = len(test\_labels)  # 总测试集数据个数  
    accur = correct/n  
    return accur  
  
  
get\_accuracy(y\_test, y\_predict)  

|

0.6974789915966386 

CART 决策树

分类与回归树（classification and regression tree, CART）同样也是应用广泛的决策树学习算法，CART 算法是按照特征划分，由树的生成和树的剪枝构成，既可以进行分类又可以用于回归，按照作用将其分为决策树和回归树，由于本实验设计为决策树的概念，所以回归树的部分有兴趣的同学可以自己查找相关资料进一步学习。

CART决策树的构建和常见的 ID3 和 C4.5 算法的流程相似，但在特征划分选择上CART选择了 基尼指数 作为划分标准。数据集 D$D$ 的纯度可用基尼值来度量：

Gini(D)=|y|∑y=1∑k′≠kpkp′k(7)

$$(7)Gini(D)=∑y=1|y|∑k′≠kpkpk′$$

基尼指数表示随机抽取两个样本，两个样本类别不一致的概率，基尼指数越小则数据集的纯度越高。同样对于每一个特征值的基尼指数计算，其和 ID3 、 C4.5 相似，定义为：

GiniValue(D,a)=M∑m=1|Dm||D|Gini(Dm)(8)

$$(8)GiniValue(D,a)=∑m=1M|Dm||D|Gini(Dm)$$

在进行特征划分的时候，选择特征中基尼值最小的作为最优特征划分点。

实际上，在应用过程中，更多的会使用 基尼指数 对特征划分点进行决策，最重要的原因是计算复杂度相较于 ID3 和 C4.5 小很多（没有对数运算）。

拓展阅读：

• 决策树- 维基百科