划分聚类，顾名思义，通过划分的方式将数据集划分为多个不重叠的子集（簇），每一个子集作为一个聚类（类别）。
在划分的过程中，首先由用户确定划分子集的个数 k$k$，然后随机选定 k$k$ 个点作为每一个子集的中心点，接下来通过迭代的方式：计算数据集中每个点与各个中心点之间的距离，更新中心点的位置；最终将数据集划分为 k$k$ 个子集，即将数据划分为 k$k$ 类。
而评估划分的好坏标准就是：保证同一划分的样本之间的差异尽可能的小，且不同划分中的样本差异尽可能的大。
K-Means 聚类方法 在划分聚类中，K-Means 是最具有代表性的算法，下面用图片的方式演示 K-Means 的基本算法流程。希望大家能通过简单的图文演示，对 K-Means 方法的原理过程产生大致的印象。
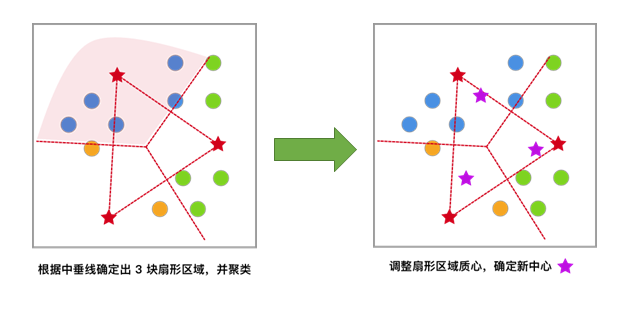
[1] 对于未聚类数据集，首先随机初始化 K 个（代表拟聚类簇个数）中心点，如图红色五角星所示。
[2] 每一个样本按照距离自身最近的中心点进行聚类，等效于通过两中心点连线的中垂线划分区域。
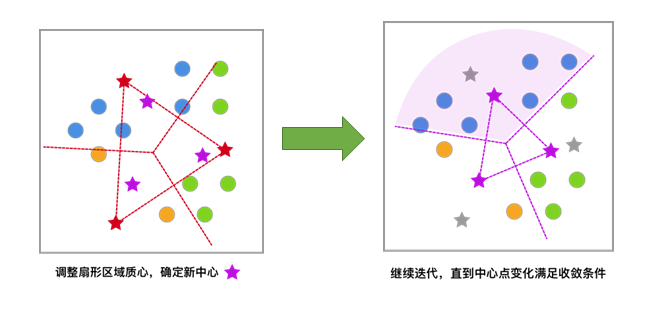
[3] 依据上次聚类结果，移动中心点到个簇的质心位置，并将此质心作为新的中心点
[4] 反复迭代，直至中心点的变化满足收敛条件（变化很小或几乎不变化），最终得到聚类结果。
在对 K-Means 有了一个直观了解后，下面我们用 Python 来进行实现。
首先通过 scikit-learn 模块的 make_blobs() 函数生成本次实验所需的示例数据。该方法可以按照我们的要求，生成特定的团状数据。
|
|
1 2 data,label = sklearn.datasets.make\_blobs(n\_samples=100,n\_features=2,centers=3,center\_box=(-10.0,10.0),random\_state=None)
|
其中参数为：
n_samples：表示生成数据总个数,默认为 100 个。
n_features：表示每一个样本的特征个数，默认为 2 个。
centers：表示中心点的个数，默认为 3 个。
center_box：表示每一个中心的边界,默认为 -10.0到10.0。
random_state：表示生成数据的随机数种子。
返回值为：
data：表示数据信息。
label：表示数据类别。
根据上面函数，在 0.0 到 10.0 上生成 200 条数据，大致包含 3 个中心。由于是用于演示聚类效果，数据标签就不是必须的了，在生成数据时赋值给 _，后面也不会使用到。
|
|
1 2 3 4 5 6 7 """构造数据 """ from sklearn.datasets import make\_blobs blobs, \_ = make\_blobs(n\_samples=200, centers=3, random\_state=18) blobs\[:10\] # 打印出前 10 条数据的信息
|
1 2 3 4 5 6 7 8 9 10 array([[ 8.28390539, 4.98011149], [ 7.05638504, 7.00948082], [ 7.43101466, -6.56941148], [ 8.20192526, -6.4442691 ], [ 3.15614247, 0.46193832], [ 7.7037692 , 6.14317389], [ 5.62705611, -0.35067953], [ 7.53828533, -4.86595492], [ 8.649291 , 3.98488194], [ 7.91651636, 4.54935348]])
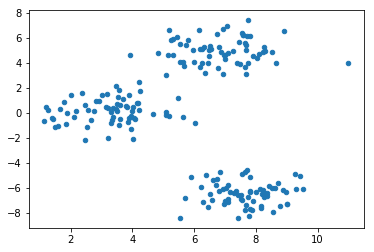
为了更加直观的查看数据分布情况，使用 matplotlib 将生成数据绘画出来。
|
|
1 2 3 4 5 6 7 """数据展示 """ %matplotlib inline import matplotlib.pyplot as plt plt.scatter(blobs\[:, 0\], blobs\[:, 1\], s=20);
|
当我们得到数据时，依照划分聚类方法的思想，首先需要随机选取 k$k$ 个点作为每一个子集的中心点。从图像中，通过肉眼很容易的发现该数据集有 3 个子集。接下来，用 numpy 模块随机生成 3 个中心点，为了更方便展示，这里我们加入了随机数种子以便每一次运行结果相同。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 """初始化中心点 """ import numpy as np def random\_k(k, data): """ 参数: k -- 中心点个数 data -- 数据集 返回: init\_centers -- 初始化中心点 """ prng = np.random.RandomState(27) # 定义随机种子 num\_feature=np.shape(data)\[1\] init\_centers = prng.randn(k, num\_feature)\*5 # 由于初始化的随机数是从-1到1，为了更加贴近数据集这里乘了一个 5 return init\_centers init\_centers=random\_k(3, blobs) init\_centers
|
1 2 3 array([[ 6.42802708, -1.51776689], [ 3.09537831, 1.97999275], [ 1.11702824, -0.27169709]])
在随机生成好中心点之后，将其在图像中表示出来，这里同样使用红色五角星表示。
|
|
1 2 3 4 5 """初始中心点展示 """ plt.scatter(blobs\[:, 0\], blobs\[:, 1\], s=20); plt.scatter(init\_centers\[:,0\], init\_centers\[:,1\], s=100, marker='\*', c="r")
|
为了找到最合适的中心点位置，需要计算每一个样本和中心点的距离，从而根据距离更新中心点位置。常见的距离计算方法有欧几里得距离和余弦相似度，本实验采用更常见且更易于理解的欧几里得距离（欧式距离）。
欧式距离源自 N$N$ 维欧氏空间中两点之间的距离公式。表达式如下:
deuc= ⎷N∑i=1(Xi−Yi)2(1)
$$(1)deuc=∑i=1N(Xi−Yi)2$$
其中：
X$X$, Y$Y$ ：两个数据点
N$N$：每个数据中有 N$N$ 个特征值，
Xi$Xi$ ：数据 X$X$ 的第 i$i$ 个特征值
将两个数据 X$X$ 和 Y$Y$ 中的每一个对应的特征值之间差值的平方，再求和，最后开平方，便是欧式距离。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 1 2 3 4 5 6 7 8 9 10 11 12 13
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 """计算欧氏距离 """ def d\_euc(x, y): """ 参数: x -- 数据 a y -- 数据 b 返回: d -- 数据 a 和 b 的欧氏距离 """ d = np.sqrt(np.sum(np.square(x - y))) return d
|
和第一章的回归算法通过减小目标函数（如：损失函数）的值拟合数据集一样，聚类算法通常也是优化一个目标函数，从而提高聚类的质量。在聚类算法中，常常使用误差的平方和 SSE（Sum of squared errors）作为度量聚类效果的标准，当 SSE 越小表示聚类效果越好。其中 SSE 表示为：
SSE(C)=K∑k=1∑xi∈Ck|xi−ck|2(2)
$$(2)SSE(C)=∑k=1K∑xi∈Ck|xi−ck|2$$
其中数据集 D={x1,x2,…,xn}$D={x1,x2,…,xn}$，xi$xi$表示每一个样本值，C$C$ 表示通过 K-Means 聚类分析后的产生类别集合 C={C1,C2,…,CK}$C={C1,C2,…,CK}$ ，ck$ck$ 是类别 Ck$Ck$ 的中心点，其中 ck$ck$ 计算方式为：
ck=∑xi∈CkxiI(Ck)(3)
$$(3)ck=∑xi∈CkxiI(Ck)$$
I(Ck)$I(Ck)$ 表示在第 k$k$ 个集合 Ck$Ck$ 中数据的个数。
当然，我们希望同最小化损失函数一样，最小化 SSE 函数，从而找出最优化的聚类模型，但是求其最小值并不容易，是一个 NP 难（非确定性多项式）的问题，其中 NP 难问题是一个经典图论问题，至今也没有找到一个完美且有效的算法。
下面我们对中心点的更新用代码的方式进行实现：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 """中心点的更新 """ def update\_center(clusters, data, centers): """ 参数: clusters -- 每一点分好的类别 data -- 数据集 centers -- 中心点集合 返回: new\_centers.reshape(num\_centers,num\_features) -- 新中心点集合 """ num\_centers = np.shape(centers)\[0\] # 中心点的个数 num\_features = np.shape(centers)\[1\] # 每一个中心点的特征数 container = \[\] for x in range(num\_centers): each\_container = \[\] container.append(each\_container) # 首先创建一个容器,将相同类别数据存放到一起 for i, cluster in enumerate(clusters): container\[cluster\].append(data\[i\]) # 为方便计算，将 list 类型转换为 np.array 类型 container = np.array(list(map(lambda x: np.array(x), container))) new\_centers = np.array(\[\]) # 创建一个容器，存放中心点的坐标 for i in range(len(container)): each\_center = np.mean(container\[i\], axis=0) # 计算每一子集中数据均值作为中心点 new\_centers = np.append(new\_centers, each\_center) return new\_centers.reshape(num\_centers, num\_features) # 以矩阵的方式返回中心点坐标
|
K-Means 算法则采用的是迭代算法，避开优化 SSE 函数，通过不断移动中心点的距离，最终达到聚类的效果。
初始化中心点：判断数据集可能被分为 k$k$ 个子集，随机生成 k$k$ 个随机点作为每一个子集的中心点。
距离计算，类别标记：样本和每一个中心点进行距离计算，将距离最近的中心点所代表的类别标记为该样本的类别。
中心点位置更新：计算每一个类别中的所有样本的均值，作为新的中心点位置。
重复 2，3 步骤，直到中心点位置不再变化。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 """K-Means 聚类 """ def kmeans\_cluster(data, init\_centers, k): """ 参数: data -- 数据集 init\_centers -- 初始化中心点集合 k -- 中心点个数 返回: centers\_container -- 每一次更新中心点的集合 cluster\_container -- 每一次更新类别的集合 """ max\_step = 50 # 定义最大迭代次数，中心点最多移动的次数。 epsilon = 0.001 # 定义一个足够小的数，通过中心点变化的距离是否小于该数，判断中心点是否变化。 old\_centers = init\_centers centers\_container = \[\] # 建立一个中心点容器，存放每一次变化后的中心点，以便后面的绘图。 cluster\_container = \[\] # 建立一个分类容器，存放每一次中心点变化后数据的类别 centers\_container.append(old\_centers) for step in range(max\_step): cluster = np.array(\[\], dtype=int) for each\_data in data: distances = np.array(\[\]) for each\_center in old\_centers: temp\_distance = d\_euc(each\_data, each\_center) # 计算样本和中心点的欧式距离 distances = np.append(distances, temp\_distance) lab = np.argmin(distances) # 返回距离最近中心点的索引，即按照最近中心点分类 cluster = np.append(cluster, lab) cluster\_container.append(cluster) new\_centers = update\_center(cluster, data, old\_centers) # 根据子集分类更新中心点 # 计算每个中心点更新前后之间的欧式距离 difference = \[\] for each\_old\_center, each\_new\_center in zip(old\_centers, new\_centers): difference.append(d\_euc(each\_old\_center, each\_new\_center)) if (np.array(difference) < epsilon).all(): # 判断每个中心点移动是否均小于 epsilon return centers\_container, cluster\_container centers\_container.append(new\_centers) old\_centers = new\_centers return centers\_container, cluster\_container
|
完成 K-Means 聚类函数后，接下来用函数得到最终中心点的位置。
|
|
1 2 3 4 5 6 7 """计算最终中心点 """ centers\_container, cluster\_container = kmeans\_cluster(blobs, init\_centers, 3) final\_center = centers\_container\[-1\] final\_cluster = cluster\_container\[-1\] final\_center
|
1 2 3 array([[ 7.67007252, -6.44697348], [ 6.83832746, 4.98604668], [ 3.28477676, 0.15456871]])
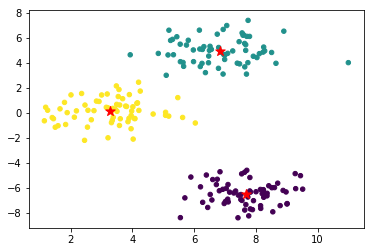
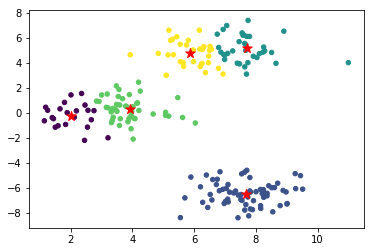
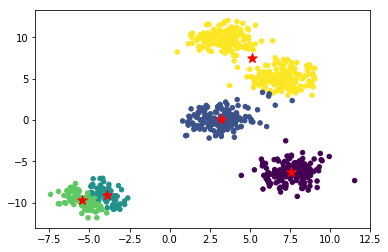
最后，我们把聚类得到的中心绘制到原图中看一看聚类效果。
|
|
1 2 3 4 5 """可视化展示 """ plt.scatter(blobs\[:, 0\], blobs\[:, 1\], s=20, c=final\_cluster); plt.scatter(final\_center\[:,0\], final\_center\[:,1\], s=100, marker='\*', c="r")
|
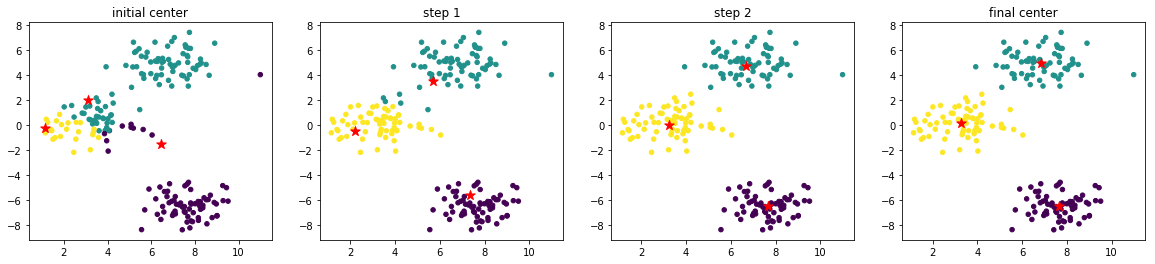
截止上小节，已经完成了 K-Means 聚类的流程。为了帮助大家理解，我们尝试将 K-Means 聚类过程中，中心点移动变化的过程绘制出来。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 num\_axes = len(centers\_container) fig, axes = plt.subplots(1, num\_axes, figsize=(20, 4)) axes\[0\].scatter(blobs\[:, 0\], blobs\[:, 1\], s=20, c=cluster\_container\[0\]) axes\[0\].scatter(init\_centers\[:, 0\], init\_centers\[:, 1\], s=100, marker='\*', c="r") axes\[0\].set\_title("initial center") for i in range(1, num\_axes-1): axes\[i\].scatter(blobs\[:, 0\], blobs\[:, 1\], s=20, c=cluster\_container\[i\]) axes\[i\].scatter(centers\_container\[i\]\[:, 0\], centers\_container\[i\]\[:, 1\], s=100, marker='\*', c="r") axes\[i\].set\_title("step {}".format(i)) axes\[-1\].scatter(blobs\[:, 0\], blobs\[:, 1\], s=20, c=cluster\_container\[-1\]) axes\[-1\].scatter(final\_center\[:, 0\], final\_center\[:, 1\], s=100, marker='\*', c="r") axes\[-1\].set\_title("final center")
|
你会惊讶的发现，对于示例数据集，虽然我们先前将最大迭代次数 max_step 设为了 50，但实际上 K-Means 迭代 3 次即收敛。原因主要有 2 点：
初始化中心点的位置很好，比较均匀分布在了数据范围中。如果初始化中心点集中分布在某一角落，迭代次数肯定会增加。
示例数据分布规整和简单，使得无需迭代多次就能收敛。
不知道你是否还记得，前面在学习分类算法 K-近邻的时候，我们讲到了 K 值的选择。而在使用 K-Means 算法聚类时，由于要提前确定随机初始化中心点的数量，同样面临着 K 值选择问题。
在前面寻找 K 值时，我们通过肉眼观察认为应该聚为 3 类。那么，如果我们设定聚类为 5 类呢？
这一次，我们尝试通过 scikit-learn 模块中的 K-Means 算法完成聚类。
|
|
1 2 3 4 from sklearn.cluster import k\_means k\_means(X, n\_clusters)
|
其中参数为：
X：表示需要聚类的数据。
n_clusters：表示聚类的个数，也就是 K 值。
返回值包含：
centroid：表示中心点坐标。
label：表示聚类后每一个样本的类别。
inertia：每一个样本与最近中心点距离的平方和，即 SSE。
|
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9
|
1 2 3 4 5 6 7 8 9 10 """用 scikit-learn 聚类并绘图 """ from sklearn.cluster import k\_means model = k\_means(blobs, n\_clusters=5) centers = model\[0\] clusters\_info = model\[1\] plt.scatter(blobs\[:, 0\], blobs\[:, 1\], s=20, c=clusters\_info) plt.scatter(centers\[:, 0\], centers\[:, 1\], s=100, marker='\*', c="r")
|
从图片上来看，聚为 5 类效果明显不如聚为 3 类的好。当然，我们提前用肉眼就能看出数据大致为 3 团。
实际的应用过程中，如果通过肉眼无法判断数据应该聚为几类？或者是高维数据无法可视化展示。面对这样的情况，我们就要从数值计算的角度去判断 K 值的大小。
接下来，将介绍一种启发式学习算法，被称之为 肘部法则，可以帮助我们选取 K 值。
使用 K-Means 算法聚类时，我们可以计算出按不同 K 值聚类后，每一个样本距离最近中心点距离的平方和 SSE。
随着 K 值增加时，也就是类别增加时，每个类别中的类内相似性也随之增加，由此造成的 SSE 的变化是单调减小的。可以想象一下，聚类类别的数量和样本的总数相同时，也就是说一个样本就代表一个类别时，这个数值会变成 0。
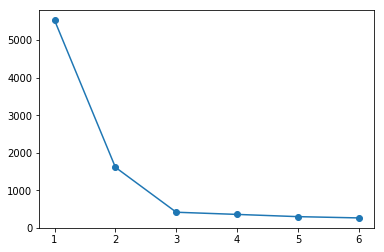
下面我们通过代码将不同的数量的聚类下，样本和最近中心点的距离和绘制出来。
|
1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11
|
1 2 3 4 5 6 7 8 9 10 11 12 index = \[\] # 横坐标数组 inertia = \[\] # 纵坐标数组 \# K 从 1~ 6 聚类 for i in range(6): model = k\_means(blobs, n\_clusters=i + 1) index.append(i + 1) inertia.append(model\[2\]) \# 绘制折线图 plt.plot(index, inertia, "-o")
|
通过上图可以看到，和预想的一样，样本距离最近中心点距离的总和会随着 K 值的增大而降低。
现在，回想本实验划分聚类中所讲评估划分的好坏标准：「保证同一划分的样本之间的差异尽可能的小，且不同划分中的样本差异尽可能的大」。
当 K 值越大时，越满足「同一划分的样本之间的差异尽可能的小」。而当 K 值越小时，越满足「不同划分中的样本差异尽可能的大畸变程度最大」。那么如何做到两端的平衡呢？
于是，我们通过 SSE 所绘制出来的图，将畸变程度最大的点称之为「肘部」 。从图中可以看到，这里的「肘部」是 K = 3（内角最小，弯曲度最大）。这也说明，将样本聚为 3 类是最佳选择（K = 2 比较接近）。这就是所谓的「肘部法则」，你明白了吗？
随着数据量的增长，分类数目增多时，由于 K-Means 中初始化中心点是随机的，常常会出现：一个较大子集有多个中心点，而其他多个较小子集公用一个中心点的问题。即算法陷入局部最优解而不是达到全局最优解的问题。
造成这种问题主要原因就是：一部分中心点在初始化时离的太近。下面我们通过例子来进一步了解。
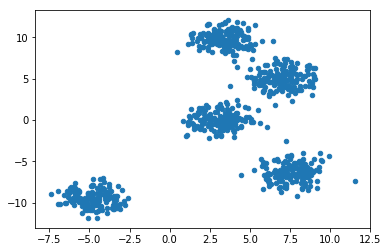
同样，我们先使用 scikit-learn 模块的 make_blobs 函数生成本次实验所需数据，本次生成 800 条数据，共 5 堆。
|
|
1 2 3 4 5 6 """生成数据并展示 """ blobs\_plus, \_ = make\_blobs(n\_samples=800, centers=5, random\_state=18) # 生成数据 plt.scatter(blobs\_plus\[:, 0\], blobs\_plus\[:, 1\], s=20) # 将数据可视化展示
|
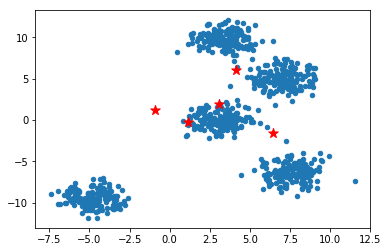
从数据点分布中可以很容易的观测出聚类数量应该为 5 类，我们先用 K-Means 中随机初始中心点的方法完成聚类：
|
|
1 2 3 4 5 km\_init\_center=random\_k(5, blobs\_plus) plt.scatter(blobs\_plus\[:, 0\], blobs\_plus\[:, 1\], s=20); plt.scatter(km\_init\_center\[:,0\], km\_init\_center\[:,1\], s=100, marker='\*', c="r")
|
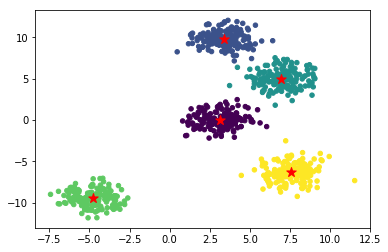
用传统的 K-Means 算法，将数据集进行聚类，聚类数量为 5。
|
|
1 2 3 4 5 6 km\_centers, km\_clusters = kmeans\_cluster(blobs\_plus, km\_init\_center, 5) km\_final\_center = km\_centers\[-1\] km\_final\_cluster = km\_clusters\[-1\] plt.scatter(blobs\_plus\[:, 0\], blobs\_plus\[:, 1\], s=20, c=km\_final\_cluster) plt.scatter(km\_final\_center\[:, 0\], km\_final\_center\[:, 1\], s=100, marker='\*', c="r")
|
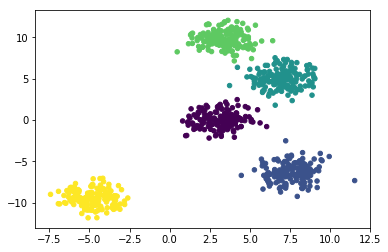
通过传统 K-Means 算法聚类后，你会发现聚类效果和我们预想不同，我们预想的结果应该是下面这样的：
|
|
1 2 plt.scatter(blobs\_plus\[:, 0\], blobs\_plus\[:, 1\], s=20, c=\_)
|
对比 K-Means 聚类和预想聚类的两张图，可以直观的看出 K-Means 算法显然没有达到最优的聚类效果，出现了本章开头所提到的局部最优解的问题。
对于局部最优问题是可以通过 SSE 来解决的，即在同一数据集上运行多次 K-Means 算法聚类，之后选取 SSE 最小的那次作为最终的聚类结果。虽然通过 SSE 找到最优解十分困难，但通过 SSE 判断最优解是十分容易的。
但当遇到更大的数据集，每一次 K-Means 算法会花费大量时间时，如果使用多次运行通过 SSE 来判断最优解，显然不是好的选择。是否有一种方法在初始化中心点时，就能有效避免局部最优问题的出现呢？
在 K-Means 的基础上，D.Arthur 等人在 2007 年提出了 K-Means++ 算法。其中 K-Means++ 算法主要针对初始化中心点问题进行改进，这样就可以从源头上解决局部最优解的问题。
K-Means++ 相较于 K-Means 在初始化中心点上做了改进，在其他方面和 K-Means 相同。
在数据集中随机选择一个样本点作为第一个初始化的聚类中心。
计算样本中的非中心点与最近中心点之间的距离 D(x)$D(x)$ 并保存于一个数组里，将数组中的这些距离加起来得到 Sum(D(x))$Sum(D(x))$。
取一个落在 Sum(D(x))$Sum(D(x))$范围中的随机值 R$R$ ，重复计算 R=R−D(x)$R=R−D(x)$ 直至得到 R≤0$R≤0$ ，选取此时的点作为下一个中心点。
重复 2,3 步骤，直到 K$K$ 个聚类中心都被确定。
对 K$K$ 个初始化的聚类中心，利用 K-Means 算法计算最终的聚类中心。
看完整个算法流程，可能会出现一个疑问：为避免初始点距离太近，直接选取距离最远的点不就好了，为什么要引入一个随机值 R$R$ 呢？
其实当采用直接选取距离最远的点作为初始点的方法，会容易受到数据集中离群点的干扰。采用引入随机值 R$R$ 的方法避免数据集中所包含的离群点对算法思想中要选择相距最远的中心点的目标干扰。
相对于正常的数据点，离群点所计算得出的 D(x)$D(x)$ 距离一定比较大，这样在选取的过程中，它被选中的概率也就相对较大，但是离群点在整个数据集中只占一小部分，大部分依然是正常的点，这样离群点由于距离大而造成的概率大，就被正常点的数量大给平衡掉。从而保证了整个算法的平衡性。
K-Means++ 在初始化样本点之后，计算其他样本与其最近的中心点距离之和，以备下一个中心点的选择，下面用 Python 来进行实现：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 def get\_sum\_dis(centers, data): """ 参数: centers -- 中心点集合 data -- 数据集 返回: np.sum(dis\_container) -- 样本距离最近中心点的距离之和 dis\_container -- 样本距离最近中心点的距离集合 """ dis\_container = np.array(\[\]) for each\_data in data: distances = np.array(\[\]) for each\_center in centers: temp\_distance = d\_euc(each\_data, each\_center) # 计算样本和中心点的欧式距离 distances = np.append(distances, temp\_distance) lab = np.min(distances) dis\_container = np.append(dis\_container, lab) return np.sum(dis\_container), dis\_container
|
接下来，我们初始化中心点：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 """K-Means++ 初始化中心点 """ def get\_init\_center(data, k): """ 参数: data -- 数据集 k -- 中心点个数 返回: np.array(center\_container) -- 初始化中心点集合 """ seed = np.random.RandomState(20) p = seed.randint(0, len(data)) first\_center = data\[p\] center\_container = \[\] center\_container.append(first\_center) for i in range(k-1): sum\_dis, dis\_con = get\_sum\_dis(center\_container, data) r = np.random.randint(0, sum\_dis) for j in range(len(dis\_con)): r = r - dis\_con\[j\] if r <= 0: center\_container.append(data\[j\]) break else: pass return np.array(center\_container)
|
实现 K-Means++ 初始化中心点函数之后，根据生成数据，得到初始化的中心点坐标。
|
|
1 2 3 plus\_init\_center = get\_init\_center(blobs\_plus, 5) plus\_init\_center
|
1 2 3 4 5 array([[ 4.1661903 , 0.81807492], [ 8.9161603 , 5.58757202], [ 7.62699601, 2.3492678 ], [-3.42049424, -9.57117787], [ 3.35681598, -0.54000802]])
为了让你更清晰的看到 K-Means++ 初始化中心点的过程，我们用 matplotlib 进行展示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 num = len(plus\_init\_center) fig, axes = plt.subplots(1, num, figsize=(25, 4)) axes\[0\].scatter(blobs\_plus\[:, 0\], blobs\_plus\[:, 1\], s=20, c="b") axes\[0\].scatter(plus\_init\_center\[0, 0\], plus\_init\_center\[0, 1\], s=100, marker='\*', c="r") axes\[0\].set\_title("first center") for i in range(1, num): axes\[i\].scatter(blobs\_plus\[:, 0\], blobs\_plus\[:, 1\], s=20, c="b") axes\[i\].scatter(plus\_init\_center\[:i+1, 0\], plus\_init\_center\[:i+1, 1\], s=100, marker='\*', c="r") axes\[i\].set\_title("step{}".format(i)) axes\[-1\].scatter(blobs\_plus\[:, 0\], blobs\_plus\[:, 1\], s=20, c="b") axes\[-1\].scatter(plus\_init\_center\[:, 0\], plus\_init\_center\[:, 1\], s=100, marker='\*', c="r") axes\[-1\].set\_title("final center")
|
通过上图可以看到点的变化，即除了最初随机选择点之外，之后的每一个点都是尽可能选择远一些的点。这样就很好的保证初始中心点的分散。
通过多次执行代码可以看到，使用 K-Means++ 同样可能出现两个中心点较近的情况，因此，在极端情况也可能出现局部最优的问题。但相比于 K-Means 算法的随机选取，K-Means++ 的初始化中心点会在很大程度上降低局部最优问题出现的概率。
在通过 K-Means++ 算法初始化中心点后，下面我们通过 K-Means 算法对数据进行聚类。
|
|
1 2 3 4 5 6 7 plus\_centers, plus\_clusters = kmeans\_cluster(blobs\_plus, plus\_init\_center, 5) plus\_final\_center = plus\_centers\[-1\] plus\_final\_cluster = plus\_clusters\[-1\] plt.scatter(blobs\_plus\[:, 0\], blobs\_plus\[:, 1\], s=20, c=plus\_final\_cluster) plt.scatter(plus\_final\_center\[:, 0\], plus\_final\_center\[:, 1\], s=100, marker='\*', c="r")
|
在 K-Means++ 算法中，我们依旧无法完全避免随机选择中心点带来的不稳定性，所以偶尔也会得到不太好的结果。当然，K-Means++ 算法得到不太好的聚类的概率远小于 K-Means 算法。所以，如果你并没有得到一个较好的聚类效果，可以再次初始化中心点尝试。
在「大数据」如此火的时代，K-Means 算法是否还能一如既往优秀的处理大数据呢？现在我们重新回顾下 K-Means 的算法原理：首先，计算每一个样本同所有中心点的距离，通过比较找到最近的中心点，将距离最近中心点的距离进行存储并归类。然后通过相同类别样本的特征值，更新中心点的位置。至此完成一次迭代，经过多次迭代后最终进行聚类。
通过上面的表述，你是否感觉到不断计算距离的过程，涉及到的计算量有多大呢？那么，设想一下数据量达到十万，百万，千万级别，且如果每一条数据有上百个特征，这将会消耗大量的计算资源。
为了解决大规模数据的聚类问题，我们就可以使用 K-Means 的另外一个变种 Mini Batch K-Means 来完成。
其算法原理也十分简单：在每一次迭代过程中，从数据集中随机抽取一部分数据形成小批量数据集，用该部分数据集进行距离计算和中心点的更新。由于每一次都是随机抽取，所以每一次抽取的数据能很好的表现原本数据集的特性。
下面，我们生成一组测试数据，并测试 K-Means 算法和 Mini Batch K-Means 在同一组数据上聚类时间和 SSE 上的差异。由于 scikit-learn 中 MiniBatchKMeans() 和 KMeans() 方法的参数几乎一致，这里就不再赘述了。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 import time from sklearn.cluster import MiniBatchKMeans, KMeans test\_data, \_ = make\_blobs(2000, n\_features=2, cluster\_std=2, centers=5) km = KMeans(n\_clusters=5) mini\_km = MiniBatchKMeans(n\_clusters=5) fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 5)) for i, model in enumerate(\[km, mini\_km\]): t0 = time.time() model.fit(test\_data) t1 = time.time() t = t1 - t0 sse = model.inertia\_ axes\[i\].scatter(test\_data\[:, 0\], test\_data\[:, 1\], c=model.labels\_) axes\[i\].set\_xlabel("time: {:.4f} s".format(t)) axes\[i\].set\_ylabel("SSE: {:.4f}".format(sse)) axes\[0\].set\_title("K-Means") axes\[1\].set\_title("Mini Batch K-Means")
|
以上是对 2000 条数据分别用 K-Means 和 Mini Batch K-Means进行聚类，从图像中可以看出，Mini Batch K-Means 在训练时间上明显比 K-Means 快（大于 2 倍不等），且聚类得到的 SSE 值比较接近。
拓展阅读：
# cluster , k-means , machine learning , python
Text(0.5, 1.0, ‘final center’)
Text(0.5, 1.0, ‘final center’)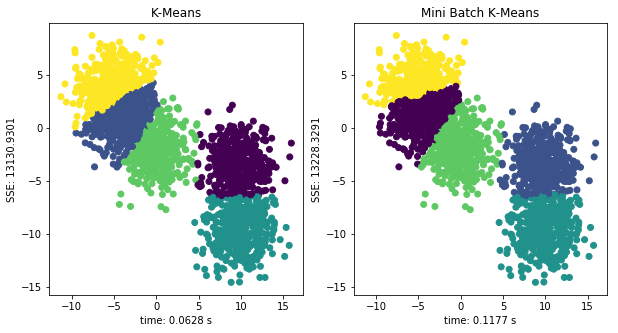
Text(0.5, 1.0, ‘Mini Batch K-Means’)
